The text of the work is placed without images and formulas.
The full version of the work is available in the "Job Files" tab in PDF format
Introduction
Transformation of graphs of a function is one of the basic mathematical concepts directly related to practical activities. The transformation of graphs of functions is first encountered in algebra grade 9 when studying the topic "Quadratic function". The quadratic function is introduced and studied in close connection with quadratic equations and inequalities. Also, many mathematical concepts are considered by graphical methods, for example, in grades 10-11, the study of a function makes it possible to find the domain of definition and the scope of the function, the areas of decrease or increase, asymptotes, intervals of constancy, etc. This important question is also submitted to the GIA. It follows that the construction and transformation of function graphs is one of the main tasks of teaching mathematics at school.
However, to plot many functions, a number of methods can be used to facilitate the construction. The above defines relevance research topics.
Object of study is the study of the transformation of graphs in school mathematics.
Subject of study - the process of constructing and transforming function graphs in a secondary school.
problem question: is it possible to build a graph of an unfamiliar function, having the skill of transforming graphs of elementary functions?
Target: plotting a function in an unfamiliar situation.
Tasks:
1. Analyze the educational material on the problem under study. 2. Identify schemes for transforming function graphs in a school mathematics course. 3. Select the most effective methods and tools for constructing and converting function graphs. 4. Be able to apply this theory in solving problems.
Necessary basic knowledge, skills, abilities:
Determine the value of the function by the value of the argument in various ways of specifying the function;
Build graphs of the studied functions;
Describe the behavior and properties of functions from the graph and, in the simplest cases, from the formula, find the largest and smallest values from the graph of the function;
Descriptions with the help of functions of various dependencies, their representation graphically, interpretation of graphs.
Main part
Theoretical part
As the initial graph of the function y = f(x), I will choose a quadratic function y=x 2 . I will consider cases of transformation of this graph associated with changes in the formula that defines this function and draw conclusions for any function.
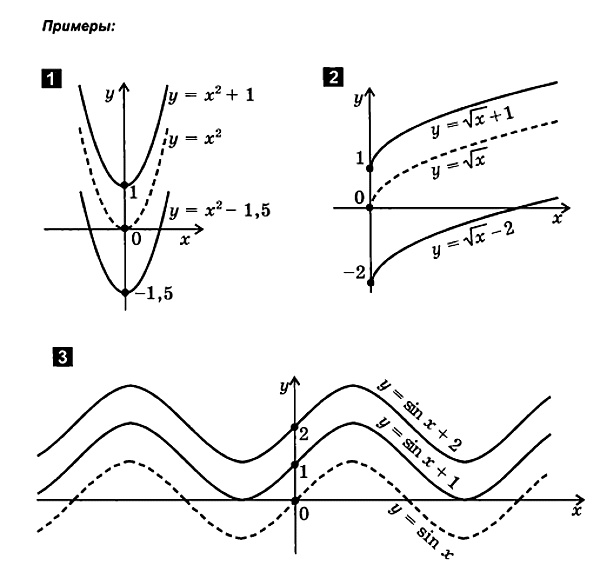
1. Function y = f(x) + a
In the new formula, the function values (the coordinates of the graph points) are changed by the number a, compared to the "old" function value. This leads to a parallel translation of the graph of the function along the OY axis:
up if a > 0; down if a< 0.
OUTPUT
Thus, the graph of the function y=f(x)+a is obtained from the graph of the function y=f(x) by means of parallel translation along the y-axis by a units up if a > 0, and by a units down if a< 0.
2. Function y = f(x-a),
In the new formula, the argument values (the abscissas of the graph points) are changed by the number a, compared to the "old" argument value. This leads to a parallel transfer of the graph of the function along the OX axis: to the right if a< 0, влево, если a >0.
OUTPUT
So the graph of the function y= f(x - a) is obtained from the graph of the function y=f(x) by parallel translation along the abscissa axis by a units to the left if a > 0, and by a units to the right if a< 0.
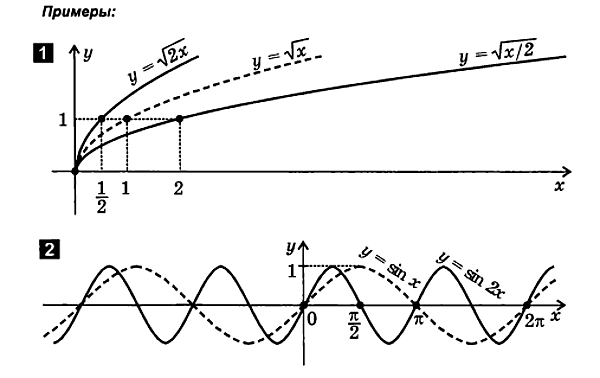
3. Function y = k f(x), where k > 0 and k ≠ 1
In the new formula, the function values (the coordinates of the graph points) change k times compared to the "old" function value. This leads to: 1) "stretching" from the point (0; 0) along the OY axis by k times, if k > 1, 2) "compression" to the point (0; 0) along the OY axis by a factor of 0, if 0< k < 1.
OUTPUT
Therefore: to build a graph of the function y = kf(x), where k > 0 and k ≠ 1, you need to multiply the ordinates of the points of the given graph of the function y = f(x) by k. Such a transformation is called stretching from the point (0; 0) along the OY axis by k times if k > 1; contraction to the point (0; 0) along the OY axis by a factor if 0< k < 1.
4. Function y = f(kx), where k > 0 and k ≠ 1
In the new formula, the values of the argument (the abscissas of the graph points) change k times compared to the "old" value of the argument. This leads to: 1) “stretching” from the point (0; 0) along the OX axis by 1/k times if 0< k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.
OUTPUT
And so: to build a graph of the function y = f(kx), where k > 0 and k ≠ 1, you need to multiply the abscissas of the points of the given graph of the function y=f(x) by k. Such a transformation is called stretching from the point (0; 0) along the OX axis by 1/k times if 0< k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.
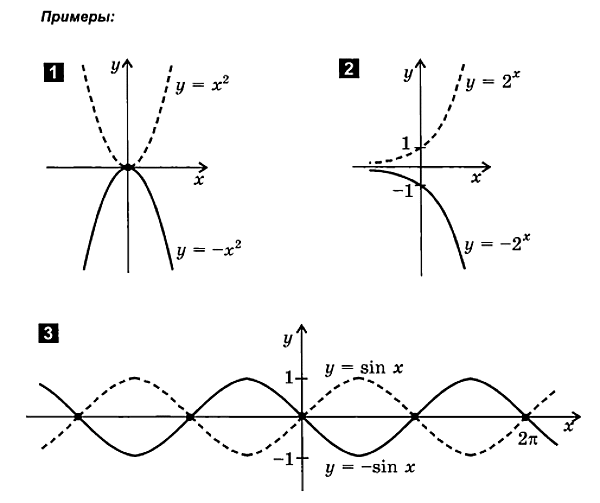
5. Function y = - f (x).
In this formula, the values of the function (the coordinates of the graph points) are reversed. This change results in a symmetrical display of the original graph of the function about the x-axis.
OUTPUT
To build a graph of the function y = - f (x), you need a graph of the function y = f (x)
reflect symmetrically about the OX axis. Such a transformation is called a symmetry transformation about the OX axis.
6. Function y = f (-x).
In this formula, the values of the argument (the abscissas of the graph points) are reversed. This change results in a symmetrical display of the original function graph with respect to the OY axis.
An example for the function y \u003d - x² this transformation is not noticeable, since this function is even and the graph does not change after the transformation. This transformation is visible when the function is odd and when neither even nor odd.
7. Function y = |f(x)|.
In the new formula, the function values (the coordinates of the graph points) are under the module sign. This leads to the disappearance of parts of the graph of the original function with negative ordinates (that is, those located in the lower half-plane relative to the Ox axis) and a symmetrical display of these parts relative to the Ox axis.
8. Function y= f (|x|).
In the new formula, the argument values (the abscissas of the graph points) are under the module sign. This leads to the disappearance of parts of the graph of the original function with negative abscissas (that is, those located in the left half-plane relative to the OY axis) and their replacement with parts of the original graph that are symmetrical about the OY axis.
Practical part
Consider a few examples of the application of the above theory.
EXAMPLE 1.
Solution. Let's transform this formula:
1) Let's build a graph of the function
EXAMPLE 2.
Plot the function given by the formula
Solution. We transform this formula by highlighting the square of the binomial in this square trinomial:
1) Let's build a graph of the function
2) Perform a parallel transfer of the constructed graph to the vector
EXAMPLE 3.
TASK FROM THE USE Plotting a piecewise function
Function graph Function graph y=|2(x-3)2-2|; one
Which of these functions have an inverse? For such functions find inverse functions:
4.12. but) |
y=x; |
b) y = 6 −3x; |
|||||
d) y = |
e) y \u003d 2 x 3 +5; |
||||||
4.13. but) |
y = 4x − 5 ; |
y \u003d 9 - 2 x - x 2; |
|||||
y = sign x ; |
y=1 + lg(x + 2) ; |
||||||
y = 2 x 2 +1 ; |
|||||||||
x − 2 |
|||||||||
at x< 0 |
|||||||||
c) y = |
−x |
||||||||
for x ≥ 0 |
|||||||||
Find out which of these functions are monotonic, which are strictly monotonic, and which are bounded:
4.14. but) |
f (x) = c, c R ; |
b) f (x) \u003d cos 2 x; |
c) f (x) \u003d arctg x; |
|||||||||||||
d) f (x) \u003d e 2 x; |
e) f (x) \u003d -x 2 + 2 x; |
e) f(x) = |
||||||||||||||
2x+5 |
||||||||||||||||
y = ctg7 x . |
||||||||||||||||
4.15. but) |
f(x) = 3−x |
b) f(x) = |
f(x)= |
x + 3 |
||||||||||||
x+6 |
||||||||||||||||
x< 0, |
3x+5 |
|||||||||||||||
d) f (x) \u003d 3 x 3 - x; |
− 10 at |
f(x)= |
||||||||||||||
e) f(x) = |
x 2 at |
x ≥ 0; |
x+1 |
|||||||||||||
f(x) = tg(sinx). |
||||||||||||||||
Recall that the graph of the function f (x) in the Cartesian rectangular coordinate system Oxy is the set of all points in the plane with coordinates (x, f (x)).
Often the graph of the function y \u003d f (x) can be built using transformations (shift, stretching) of the graph of some already known function.

In particular, from the graph of the function y \u003d f (x), the graph of the function is obtained:
1) y \u003d f (x) + a - shift along the Oy axis by a units (up if a > 0, and down if a< 0 ;
2) y \u003d f (x − b) - shift along the Ox axis by b units (to the right, if b > 0,
and to the left if b< 0 ;
3) y \u003d kf (x) - by stretching along the Oy axis by k times;
4) y \u003d f (mx) - compression along the Ox axis by m times;
5) y \u003d - f (x) - symmetrical reflection about the axis Ox;
6) y \u003d f (−x) - symmetrical reflection about the axis Oy;
7) y \u003d f (x), as follows: the part of the graph located not
below the Ox axis, remains unchanged, and the “lower” part of the graph is reflected symmetrically about the Ox axis;
8) y = f (x ) , as follows: the right side of the graph (for x ≥ 0 )
remains unchanged, and instead of "left" a symmetrical reflection of the "right" about the axis Oy is built.
The main elementary functions are called:
1) constant function y = c;
2) power function y = x α , α R ;
3) exponential function y \u003d a x, a ≠ 0, a ≠1;
4) logarithmic function y = log a x , a > 0, a ≠ 1 ;
5) trigonometric functions y = sin x , y = cos x , y = tg x ,
y = ctg x , y = sec x (where sec x = cos 1 x ), y = cosec x (where cosec x = sin 1 x );
6) inverse trigonometric functions y \u003d arcsin x, y \u003d arccos x, y \u003d arctg x, y \u003d arcctg x.
elementary functions called functions obtained from the basic elementary functions with the help of a finite number of arithmetic operations (+, − , ÷) and compositions (i.e., the formation of complex functions f g ).

Example 4.6. Plot a function
1) y \u003d x 2 + 6 x + 7; 2) y = −2sin 4 x .
Solution: 1) by highlighting the full square, the function is converted to the form y = (x +3) 2 − 2, so the graph of this function can be obtained from the graph of the function y = x 2 . It is enough to first shift the parabola y \u003d x 2 three units to the left (we get the graph of the function y \u003d (x +3) 2), and then two units down (Fig. 4.1);
standard |
sinusoid |
y = sin x |
four times along the axis |
Ox, |
|||||||
we get the graph of the function y \u003d sin 4 x (Fig. 4.2). |
|||||||||||
y=sin4x |
|||||||||||
y=sin x |
|||||||||||
Stretching the resulting graph twice along the Oy axis, we get the graph of the function y \u003d 2sin 4 x (Fig. 4.3). It remains to reflect the last graph relative to the Ox axis. The result will be the desired graph (see Fig. 4.3).

y=2sin4x |
|||||||
y=–2sin4x
Tasks for independent solution
Construct graphs of the following functions, based on the graphs of the main elementary functions:
4.16. a) y \u003d x 2 -6 x +11;
4.17. a) y = −2sin(x −π ) ;
4.18. a) y = − 4 x −1 ;
4.19. a) y = log 2 (−x ) ;
4.20. a) y = x +5 ;
4.21. a) y \u003d tg x;
4.22. a) y = sign x ;
4.23. a) y = x x + + 4 2 ;
y = 3 - 2 x - x 2 .
y = 2 cos 2 x .
Function Graph Transformation
In this article, I will introduce you to linear transformations of function graphs and show you how to use these transformations to get a function graph from a function graph. ![]()
A linear transformation of a function is a transformation of the function itself and/or its argument to the form ![]() , as well as a transformation containing the module of the argument and/or functions.
, as well as a transformation containing the module of the argument and/or functions.
The following actions cause the greatest difficulties in plotting graphs using linear transformations:
AND It is on these points that we will dwell in more detail.
Let's take a closer look at the function
![]()
It is based on a function. Let's call her basic function.
When plotting a function ![]() we make transformations of the graph of the base function .
we make transformations of the graph of the base function .
If we were to transform the function ![]() in the same order in which its value was found for a certain value of the argument, then
in the same order in which its value was found for a certain value of the argument, then
Let's consider what types of linear argument and function transformations exist, and how to perform them.
Argument transformations.
1. f(x) f(x+b)
1. We build a graph of a function
2. We shift the graph of the function along the OX axis by |b| units
Let's plot the function
1. We plot the function
2. Shift it 2 units to the right:

2. f(x) f(kx)
1. We build a graph of a function
2. Divide the abscissas of the graph points by k, leave the ordinates of the points unchanged.
Let's plot the function.
1. We plot the function
2. Divide all abscissas of the graph points by 2, leave the ordinates unchanged:

3. f(x) f(-x)
1. We build a graph of a function
2. We display it symmetrically about the OY axis.
Let's plot the function.
1. We plot the function
2. We display it symmetrically about the OY axis:

4. f(x) f(|x|)
1. We plot the function
2. We erase the part of the graph located to the left of the OY axis, the part of the graph located to the right of the OY axis We complete it symmetrically about the OY axis:
The graph of the function looks like this:

Let's plot the function
1. We build a function graph (this is a function graph shifted along the OX axis by 2 units to the left):

2. Part of the graph located to the left of the OY (x<0) стираем:
3. The part of the graph located to the right of the OY axis (x>0) is completed symmetrically with respect to the OY axis:

Important! The two main rules for argument conversion.
1. All argument transformations are performed along the OX axis
2. All transformations of the argument are performed "vice versa" and "in reverse order".
For example, in a function, the sequence of argument transformations is as follows:
1. We take the module from x.
2. Add the number 2 to the modulo x.
But we did the plotting in the reverse order:
First, we performed the transformation 2. - shifted the graph by 2 units to the left (that is, the abscissas of the points were reduced by 2, as if "vice versa")
Then we performed the transformation f(x) f(|x|).
Briefly, the sequence of transformations is written as follows:

Now let's talk about function transformation . Transformations are being made
1. Along the OY axis.
2. In the same sequence in which the actions are performed.
These are the transformations:
1. f(x)f(x)+D
2. Shift it along the OY axis by |D| units
Let's plot the function
1. We plot the function
2. Move it along the OY axis by 2 units up:

2. f(x)Af(x)
1. We plot the function y=f(x)
2. We multiply the ordinates of all points of the graph by A, we leave the abscissas unchanged.
Let's plot the function
1. Graph the function
2. We multiply the ordinates of all points of the graph by 2:

3.f(x)-f(x)
1. We plot the function y=f(x)
Let's plot the function.
1. We build a function graph.
2. We display it symmetrically about the OX axis.

4. f(x)|f(x)|
1. We plot the function y=f(x)
2. The part of the graph located above the OX axis is left unchanged, the part of the graph located below the OX axis is displayed symmetrically about this axis.
Let's plot the function
1. We build a function graph. It is obtained by shifting the graph of the function along the OY axis by 2 units down:

2. Now the part of the graph located below the OX axis will be displayed symmetrically with respect to this axis:

And the last transformation, which, strictly speaking, cannot be called a function transformation, since the result of this transformation is no longer a function:
|y|=f(x)
1. We plot the function y=f(x)
2. We erase the part of the graph located below the OX axis, then we complete the part of the graph located above the OX axis symmetrically about this axis.
Let's build a graph of the equation
1. We build a function graph:

2. We erase the part of the graph located below the OX axis:

3. The part of the graph located above the OX axis is completed symmetrically about this axis.
And finally, I suggest you watch the VIDEO LESSON in which I show a step-by-step algorithm for plotting a function graph
![]()
The graph of this function looks like this:

Hypothesis: If you study the movement of the graph during the formation of the equation of functions, you will notice that all graphs obey common laws, therefore, you can formulate general laws regardless of the functions, which will not only facilitate the construction of graphs of various functions, but also use them in solving problems.
Purpose: To study the movement of graphs of functions:
1) The task of studying literature
2) Learn to build graphs of various functions
3) Learn to convert graphs of linear functions
4) Consider the use of graphs in solving problems
Object of study: Graphs of functions
Subject of research: Movements of graphs of functions
Relevance: The construction of function graphs, as a rule, takes a lot of time and requires attention from the student, but knowing the rules for transforming function graphs and graphs of basic functions, you can quickly and easily build function graphs, which will allow you not only to complete tasks for plotting function graphs, but also solve related problems (to find the maximum (minimum height of time and meeting point))
This project is useful to all students of the school.
Literature review:
The literature discusses ways to construct a graph of various functions, as well as examples of the transformation of graphs of these functions. Graphs of almost all main functions are used in various technical processes, which makes it possible to more clearly present the course of the process and program the result
Permanent function. This function is given by the formula y = b, where b is some number. The graph of a constant function is a straight line parallel to the x-axis and passing through the point (0; b) on the y-axis. The graph of the function y \u003d 0 is the abscissa axis.
Types of function 1Direct proportionality. This function is given by the formula y \u003d kx, where the coefficient of proportionality k ≠ 0. The direct proportionality graph is a straight line passing through the origin.
Linear function. Such a function is given by the formula y = kx + b, where k and b are real numbers. The graph of a linear function is a straight line.
Linear function graphs can intersect or be parallel.
So, the lines of the graphs of linear functions y \u003d k 1 x + b 1 and y \u003d k 2 x + b 2 intersect if k 1 ≠ k 2; if k 1 = k 2 , then the lines are parallel.
2 Inverse proportionality is a function that is given by the formula y \u003d k / x, where k ≠ 0. K is called the inverse proportionality coefficient. The inverse proportionality graph is a hyperbola.
The function y \u003d x 2 is represented by a graph called a parabola: on the interval [-~; 0] the function is decreasing, on the interval the function is increasing.
The function y \u003d x 3 increases along the entire number line and is graphically represented by a cubic parabola.
Power function with natural exponent. This function is given by the formula y \u003d x n, where n is a natural number. Graphs of a power function with a natural exponent depend on n. For example, if n = 1, then the graph will be a straight line (y = x), if n = 2, then the graph will be a parabola, etc.
A power function with a negative integer exponent is represented by the formula y \u003d x -n, where n is a natural number. This function is defined for all x ≠ 0. The graph of the function also depends on the exponent n.
Power function with a positive fractional exponent. This function is represented by the formula y \u003d x r, where r is a positive irreducible fraction. This function is also neither even nor odd.
Graph-line that displays the relationship of dependent and independent variables on the coordinate plane. The graph serves to visually display these elements.
An independent variable is a variable that can take on any value in the scope of the functions (where the given function makes sense (cannot be divided by zero))
To plot a function graph,
1) Find ODZ (range of acceptable values)
2) take some arbitrary values for the independent variable
3) Find the value of the dependent variable
4) Build a coordinate plane, mark these points on it
5) Connect their lines if necessary, investigate the resulting graph. Transformation of graphs of elementary functions.
Graph Conversion
In their pure form, the basic elementary functions are, unfortunately, not so common. Much more often one has to deal with elementary functions obtained from basic elementary functions by adding constants and coefficients. Graphs of such functions can be built by applying geometric transformations to the graphs of the corresponding basic elementary functions (or by switching to a new coordinate system). For example, a quadratic function formula is a quadratic parabola formula, compressed three times relative to the ordinate axis, symmetrically displayed relative to the abscissa axis, shifted against the direction of this axis by 2/3 units and shifted along the direction of the ordinate axis by 2 units.
Let's understand these geometric transformations of a function graph step by step using specific examples.
With the help of geometric transformations of the graph of the function f (x), a graph of any function of the form formula can be constructed, where the formula is the compression or expansion coefficients along the oy and ox axes, respectively, the minus signs in front of the coefficients formula and formula indicate a symmetrical display of the graph relative to the coordinate axes , a and b define the shift relative to the abscissa and ordinate axes, respectively.
Thus, there are three types of geometric transformations of the function graph:
The first type is scaling (compression or expansion) along the abscissa and ordinate axes.
The need for scaling is indicated by formula coefficients other than one, if the number is less than 1, then the graph is compressed relative to oy and stretched relative to ox, if the number is greater than 1, then we stretch along the ordinate axis and shrink along the abscissa axis.
The second type is a symmetrical (mirror) display with respect to the coordinate axes.
The need for this transformation is indicated by the minus signs in front of the coefficients of the formula (in this case, we display the graph symmetrically with respect to the ox axis) and the formula (in this case, we display the graph symmetrically with respect to the y axis). If there are no minus signs, then this step is skipped.
DAGESTAN INSTITUTE FOR PROFESSIONAL DEVELOPMENT
PEDAGOGICAL STAFF
DEPARTMENT OF PHYSICAL AND MATHEMATICAL EDUCATION AND ICT
Project
on the topic:
« Construction and p reforms
function graphs
in school mathematics »
Rabadanova P.A.
mathematic teacher
MBOU "Kochubey secondary school"
Tarumovsky district
2015
1. Introduction……………………………………………………………….….3
2. Chapter I. Review of literature on the topic of the project………………………….….5
3. Chapter II. Empirical part:
3.1. Basic methods for converting function graphs……….….7
3.2. Plotting an evenAndodd functions…………….. 10
3.3. Plotting an inverse function………………………... 11
3.4. Deformation (compression and tension) of graphs………………….12
3.5. Combination of transfer, reflection and deformation………………......13
4. Tasks for independent solution………………………..…...14
5.Conclusion…………………………………………………………………15
6. Conclusions…………………………………………………………..………17
INTRODUCTION
Transformation of function graphs is one of the fundamental mathematical concepts directly related to practical activities. The graphs reflect the variability and dynamism of the real world, the mutual relations of real objects and phenomena.
The functional line is the basic topic covered in the Basic and Unified State Examinations.Also, many mathematical concepts are considered by graphical methods. For example, toquadraticthe function is introduced and studied in close connection with quadratic equations and inequalities.Hence it follows thatteaching students how to build and transform graphs of a function is one of the main tasks of teaching mathematics at school.
The study of the function makes it possible to find aboutdomain of definition and scope of the function, scopeDecreasing or increasing rates, asymptotes, intervalssign constancy, etc. However, to build a graphkov many functions can beuse a number of methodsmake it easierbuilding. Therefore, students should have the competence to build graphs according to methodological schemes.
The above definesrelevance research topics.
Object of study is the study of the transformation of functional line graphs in school mathematics.
Subject of study - the process of constructing and transforming function graphs in a secondary school.
Purpose of the study: educational - consists in identifying a methodological scheme for constructing and converting graphs of a function;developing - development of abstract, algorithmic, logical thinking, spatial imagination;educational - education of the graphic culture of schoolchildren, the formation of mental skills.
The goals led to the decision of the followingtasks:
1. Analyze the educational and methodological on the problem under study.
2. Identify methodological schemestransformation of function graphs in the school course of mathematics.
3. Select the most effective methods and meansconstruction and transformation of function graphs in a secondary schoolcontributing to: meaningful assimilation of educational material; increasing the cognitive activity of students; development of their creative abilities.
HYPOTHESIS research: the formation of graphic skills in the process of studying the functions and the education of the graphic culture of students will effective if students have a methodical scheme for constructing and transforming function graphs in a school mathematics course.
CHAPTER I . REVIEW OF LITERATURE ON THE TOPIC OF THE PROJECT.
In preparation for the project, we studied the following literature:
Sivashinsky, I. Kh. Theorems and problems in algebra, elementary functions - M., 2002. - 115 p.
Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Functions and graphs (basic techniques) - M., 1985. - 120 s
V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Elementary Mathematics - M., 2010 (reissue). - 590 p.
Kuzmin, M. K. Construction of a graph of a function - J. Mathematics at school. - 2003. - No. 5. - S. 61-62.
Shilov G.E. How to build charts? - M., 1982.
Isaac Tanatar. Geometric transformations of graphs of functions - MTsNMO, 2012
INIt is noted that the ability to “read” the behavior of a function on a certain set using a graph is used not only in the course of mathematics, but also in any practical human activity in which he has to deal with certain graphic representations of dependencies. Therefore, students should be able to determine some of its properties from the graph of a function.
The theoretical material for the transformation of graphs is strictly stated in. The technique is accompanied by illustrations with drawings, examples of varying complexity and their solutions, which makes it possible to deepen knowledge and plot complex functions.
Represents an electronic training course, the volume and content of which meet the requirements for a high school mathematics course. The theoretical material is supported by graphic animation illustrations that give a visual representation of the topic under study. The course includes three modules: a theoretical material study module, a self-examination module and a knowledge control module.
From , , methodical charting schemes, examples for independent work were used for the empirical part of the project.
Conclusions to chapter 1
The study of educational and methodical literature allowed:
1. Identify methodological schemestudying, constructing and transforming graphs of a function in a school mathematics course.
2. Select the most effective methods and meansconstruction and transformation of function graphs in school mathematics,contributing:
meaningful assimilation of educational material;
increasing the cognitive activity of students;
development of their creative abilities.
3. show that the functional line has a significant impact in the study of various concepts in mathematics.
Chapter 2. EMPIRICAL PART
In this chapter, we will consider the main methods for transforming function graphs, and give methodological schemes for constructing various combinations of graphs for various functions.
2.1. BASIC TECHNIQUES FOR FUNCTION GRAPH CONVERSION
Translation along the y-axis
f ( x ) f ( x )+ b .
Forplotting a functiony = f( x) + btraceem:
1. build a function graphy= f( x)
2. move axisabscissa on| b| units up atb>0 or at| b| eatprostrate down atb < 0. Obtained in the new systemdinat graph is the graph of a functiony = f( x) + b.
2. Transfer along axes abscissa
f ( x ) f ( x + a ) .
y = f( x+ a) traceem:

3. Plotting a function of the form y = f (- x )
f (x ) f (- x ).
To plot a functiony = f( - x) follows:
plot a functiony = f( x)
reflect it backrelative to the y-axis
the resulting graph isfunction graphy = f( - X).

4. Plotting a function of the form y= - f ( x )
f ( x ) - f ( x )
- f( x) follows:
plot a functiony= f( x)
reflect it about the x-axis
2.2. Plotting an even And odd features
When plottingFor even and odd functions, it is convenient to use the following properties:
1. Graph of an even function simmetricen relative to the y-axis.
2. The graph of an odd function is symmetrical about the origin.
To build graphs of even and odd functions, it is enough to plot only the right branch of the graph for positive values of the argument. The left branch is completed symmetrically about the origin for an odd function and about the y-axis for an even function.
To plot an even function y = f ( x ) after duet:
construct a branch of the graph of this function only inrange of positive values of the argument x≥0.
ABOUTtrace this branch about the y-axis

To plot an odd function y = f ( x ) follows:
build a graph branch of this function only inarea of positive values of the argument (х≥0).
ABOUTtrace this branch with respect to the originto the region of negative x values.

2.3. Plotting the inverse function
As already noted, the direct and inverse functionsshow the same relationship between variablesx and y, with the only difference that in the inverse function thesevariables have changed roles, which is equivalent to changingnotation of coordinate axes. Therefore, the graphthe inverse function is symmetrical to the graph of the direct functionabout the bisectorIAndIIIcoordinate angles,i.e. relatively straighty = x. Thus, we getnext rule.
To plot the function y = (x) inverse to the functiony = f( x), should be builtscheduley = f( x) and reflect it with respect to the straight line y = x.

2.4. Deformation (compression and tension) of graphs
1. Compression (expansion) of the graph along the y-axis
f ( x ) A ∙ f ( x ).
To plot a functiony= A∙ f( x) follows:

8. Compression (expansion) of the graph along the x-axis
f( x)
To plot the function y= f( x) follows:
2.5. Combination of translation, reflection and deformation
Very often when plotting function graphs forchange the combination.
Consistent application of a number of such posture techniquesallows to significantly simplify the construction of a graph usingrunning function and often reduce it in the end toconstruction of one of the simplest elementary functionstions. Consider how, in view of the foregoing, it followsbuild function graphs.
Let us note that it is timeit is advisable to carry out the simplification dock in the next successorness.
Using parity orfunction oddness.
Axes transfer.
Reflection and deformation.
The construction of the graph is performed in the reverse order.
Example.
Plot a function![]()
The construction will be carried out in the following steps:
1. plot the natural logarithm:
2. squeezeto the axisOY2 times:;
3.
display symmetricallyabout the axisOY:
;
4. move along the axisOXon the(!!!) to the right:![]() :
:

5. display symmetrically about the axisOX:
;
6. movealong the axisOY3 units up:![]() :
:

EXAMPLES OF CONSTRUCTION AND CONVERSION OF FUNCTION GRAPHS
Example 1 Plot a function.
First, draw a sine graph, its period is equal to:

function graphobtained by compressing the graphtwice to the y-axis. log .
Plot a functionat = 2 cosX.
Plot a functiony = sinx .
CONCLUSION
During the work on the project work, various educational and methodological literature on this issue were analyzed. The results of the study made it possible to identify the most characteristic positive aspects of the study, construction and transformation of graphs of a function in a school mathematics course
The main goal of the project is to develop students' skills and abilities in reading and drawing drawings, in the formation of rational methods of independent activity.
The need to improve graphic education as a whole is dictated not only by modern production requirements, but also by the role of graphics in the development of technical thinking and cognitive abilities of students. A person's ability to process graphic information is one of the indicators of his mental development. Therefore, graphic training should become an integral element of general educational training.
conclusions
Thus, the developed project "Construction and transformation of function graphs", dedicated to one of the central concepts of mathematics - functional dependence, is focused on systematization and expansion of students' knowledge. The study of specific methods for transforming function graphs is carried out in an analytical and graphical way according to strict methodological schemes. The collected material can be used in the classroom and for self-training of students. A variety of forms and methods of organization and training can be used to conduct classes.