De tekst van het werk is geplaatst zonder afbeeldingen en formules.
De volledige versie van het werk is beschikbaar op het tabblad "Taakbestanden" in PDF-formaat

Invoering

Transformatie van grafieken van een functie is een van de wiskundige basisconcepten die rechtstreeks verband houden met praktische activiteiten. De transformatie van grafieken van functies wordt voor het eerst aangetroffen in algebra graad 9 bij het bestuderen van het onderwerp "Kwadratische functie". De kwadratische functie wordt geïntroduceerd en bestudeerd in nauw verband met kwadratische vergelijkingen en ongelijkheden. Ook worden veel wiskundige concepten door grafische methoden overwogen, bijvoorbeeld in de klassen 10-11, maakt de studie van een functie het mogelijk om het definitiedomein en de reikwijdte van de functie, de gebieden van afname of toename, asymptoten, intervallen van constantheid, enz. Deze belangrijke vraag wordt ook voorgelegd aan de GIA. Hieruit volgt dat de constructie en transformatie van functiegrafieken een van de belangrijkste taken is van het wiskundeonderwijs op school.

Om echter veel functies te plotten, kunnen een aantal methoden worden gebruikt om de constructie te vergemakkelijken. Het bovenstaande definieert: relevantie onderzoeksonderwerpen.

Studieobject is de studie van de transformatie van grafieken in schoolwiskunde.

Onderwerp van studie - het proces van het construeren en transformeren van functiegrafieken in een middelbare school.

probleem vraag: is het mogelijk om een ​​grafiek van een onbekende functie te bouwen, met de vaardigheid om grafieken van elementaire functies te transformeren?

Doel: het plotten van een functie in een onbekende situatie.

Taken:

1. Analyseer het educatieve materiaal over het te bestuderen probleem. 2. Identificeer schema's voor het transformeren van functiegrafieken in een wiskundecursus op school. 3. Selecteer de meest effectieve methoden en hulpmiddelen voor het construeren en converteren van functiegrafieken. 4. Deze theorie kunnen toepassen bij het oplossen van problemen.

Benodigde basiskennis, vaardigheden, capaciteiten:

Bepaal de waarde van de functie door de waarde van het argument op verschillende manieren om de functie te specificeren;

Grafieken maken van de bestudeerde functies;

Beschrijf het gedrag en de eigenschappen van functies uit de grafiek en zoek in de eenvoudigste gevallen uit de formule de grootste en kleinste waarden uit de grafiek van de functie;

Beschrijvingen met behulp van functies van verschillende afhankelijkheden, hun grafische weergave, interpretatie van grafieken.

Grootste deel

Theoretisch gedeelte

Als de begingrafiek van de functie y = f(x), zal ik een kwadratische functie kiezen y=x 2 . Ik zal gevallen van transformatie van deze grafiek beschouwen die verband houden met veranderingen in de formule die deze functie definieert en conclusies trekken voor elke functie.

1. Functie y = f(x) + a

In de nieuwe formule worden de functiewaarden (de coördinaten van de grafiekpunten) gewijzigd met het cijfer a, ten opzichte van de "oude" functiewaarde. Dit leidt tot een parallelle vertaling van de grafiek van de functie langs de OY-as:

omhoog als a > 0; naar beneden als een< 0.

CONCLUSIE

Zo wordt de grafiek van de functie y=f(x)+a verkregen uit de grafiek van de functie y=f(x) door middel van parallelle translatie langs de y-as met a eenheden omhoog als a > 0, en door a eenheden omlaag als a< 0.

2. Functie y = f(x-a),

In de nieuwe formule worden de argumentwaarden (de abscis van de grafiekpunten) veranderd met het getal a, vergeleken met de "oude" argumentwaarde. Dit leidt tot een parallelle overdracht van de grafiek van de functie langs de OX-as: naar rechts als a< 0, влево, если a >0.

CONCLUSIE

Dus de grafiek van de functie y= f(x - a) wordt verkregen uit de grafiek van de functie y=f(x) door parallelle translatie langs de as van de abscis door een eenheid naar links als a > 0, en door een eenheid naar rechts als een< 0.

3. Functie y = k f(x), waarbij k > 0 en k ≠ 1

In de nieuwe formule veranderen de functiewaarden (de coördinaten van de grafiekpunten) k keer ten opzichte van de "oude" functiewaarde. Dit leidt tot: 1) "uitrekken" vanaf het punt (0; 0) langs de OY-as met k keer, als k > 1, 2) "compressie" tot het punt (0; 0) langs de OY-as met een factor van 0, indien 0< k < 1.

CONCLUSIE

Daarom: om een ​​grafiek te maken van de functie y = kf(x), waarbij k > 0 en k ≠ 1, moet je de ordinaat van de punten van de gegeven grafiek van de functie y = f(x) vermenigvuldigen met k. Zo'n transformatie heet uitrekken vanaf het punt (0; 0) langs de OY-as met k keer als k > 1; samentrekking tot het punt (0; 0) langs de OY-as met een factor als 0< k < 1.

4. Functie y = f(kx), waarbij k > 0 en k ≠ 1

In de nieuwe formule veranderen de waarden van het argument (de abscis van de grafiekpunten) k keer ten opzichte van de "oude" waarde van het argument. Dit leidt tot: 1) “uitrekken” vanaf het punt (0; 0) langs de OX-as met 1/k maal indien 0< k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

CONCLUSIE

En dus: om een ​​grafiek te maken van de functie y = f(kx), waarbij k > 0 en k ≠ 1, moet je de abscis van de punten van de gegeven grafiek van de functie y=f(x) vermenigvuldigen met k . Zo'n transformatie heet uitrekken vanaf het punt (0; 0) langs de OX-as met 1/k keer als 0< k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

5. Functie y = - f (x).

In deze formule zijn de waarden van de functie (de coördinaten van de grafiekpunten) omgekeerd. Deze wijziging resulteert in een symmetrische weergave van de oorspronkelijke grafiek van de functie rond de x-as.

CONCLUSIE

Om een ​​grafiek te maken van de functie y = - f (x), heb je een grafiek nodig van de functie y = f (x)

symmetrisch reflecteren om de OX-as. Zo'n transformatie wordt een symmetrietransformatie om de OX-as genoemd.

6. Functie y = f (-x).

In deze formule zijn de waarden van het argument (de abscis van de grafiekpunten) omgekeerd. Deze wijziging resulteert in een symmetrische weergave van de oorspronkelijke functiegrafiek ten opzichte van de OY-as.

Een voorbeeld voor de functie y \u003d - x² deze transformatie is niet merkbaar, omdat deze functie even is en de grafiek niet verandert na de transformatie. Deze transformatie is zichtbaar als de functie oneven is en niet even of oneven.

7. Functie y = |f(x)|.

In de nieuwe formule staan ​​de functiewaarden (de coördinaten van de grafiekpunten) onder het moduleteken. Dit leidt tot het verdwijnen van delen van de grafiek van de oorspronkelijke functie met negatieve ordinaten (dat wil zeggen, die in het onderste halve vlak ten opzichte van de Ox-as) en een symmetrische weergave van deze delen ten opzichte van de Ox-as.

8. Functie y= f (|x|).

In de nieuwe formule staan ​​de argumentwaarden (de abscis van de grafiekpunten) onder het moduleteken. Dit leidt tot het verdwijnen van delen van de grafiek van de oorspronkelijke functie met negatieve abscis (dat wil zeggen, die in het linker halve vlak ten opzichte van de OY-as) en hun vervanging door delen van de originele grafiek die symmetrisch zijn rond de OY as.

Praktijkgedeelte

Beschouw een paar voorbeelden van de toepassing van de bovenstaande theorie.

VOORBEELD 1.

Beslissing. Laten we deze formule transformeren:

1) Laten we een grafiek van de functie maken

VOORBEELD 2.

Plot de functie gegeven door de formule

Beslissing. We transformeren deze formule door het kwadraat van de binomiaal in deze vierkante trinominaal te markeren:

1) Laten we een grafiek van de functie maken

2) Voer een parallelle overdracht uit van de geconstrueerde grafiek naar de vector

VOORBEELD 3.

TAAK VAN HET GEBRUIK Een stukgewijze functie plotten

Functiegrafiek Functiegrafiek y=|2(x-3)2-2|; een

Welke van deze functies heeft een inverse? Zoek voor dergelijke functies inverse functies:

4.12. a)	y=x;					b) y = 6 −3x;
d) y =						e) y \u003d 2 x 3 +5;
4.13. a)	y = 4x − 5 ;						y \u003d 9 - 2 x - x 2;
	y = teken x ;						y=1 + lg(x + 2) ;

	y = 2 x 2 +1 ;
			x − 2
						bij x< 0
c) y =		x
						voor x ≥ 0

Zoek uit welke van deze functies monotoon zijn, welke strikt monotoon zijn en welke begrensd zijn:

4.14. a)

f (x) = c, cR;

b) f (x) \u003d cos 2 x;

c) f (x) \u003d arctg x;

d) f (x) \u003d e 2 x;

e) f (x) \u003d -x 2 + 2 x;

e) f(x) =

2x+5

y = ctg7 x .

4.15. a)

f(x) = 3− x

b) f(x) =

f(x)=

x + 3

x+6

x< 0,

3x+5

d) f (x) \u003d 3 x 3 - x;

− 10 bij

f(x)=

e) f(x) =

x 2 om

x ≥ 0;

x+1

f(x) = tg(sinx).

4.2. elementaire functies. Functie Grafiek Transformatie

Bedenk dat de grafiek van de functie f (x) in het Cartesiaanse rechthoekige coördinatenstelsel Oxy de verzameling is van alle punten in het vlak met coördinaten (x, f (x)).

Vaak kan de grafiek van de functie y \u003d f (x) worden gebouwd met behulp van transformaties (verschuiving, rekken) van de grafiek van een reeds bekende functie.

In het bijzonder wordt uit de grafiek van de functie y \u003d f (x) de grafiek van de functie verkregen:

1) y \u003d f (x) + a - verschuiving langs de Oy-as met een eenheid (omhoog als a > 0, en omlaag als a< 0 ;

2) y \u003d f (x − b) - verschuif langs de Ox-as met b-eenheden (naar rechts, als b > 0,

en naar links als b< 0 ;

3) y \u003d kf (x) - door k keer uit te rekken langs de Oy-as;

4) y \u003d f (mx) - compressie langs de Ox-as met m keer;

5) y \u003d - f (x) - symmetrische reflectie rond de as Ox;

6) y \u003d f (−x) - symmetrische reflectie rond de as Oy;

7) y \u003d f (x), als volgt: het deel van de grafiek dat zich niet bevindt

onder de os-as, blijft ongewijzigd, en het "onderste" deel van de grafiek wordt symmetrisch om de os-as gereflecteerd;

8) y = f (x ), als volgt: de rechterkant van de grafiek (voor x ≥ 0 )

blijft ongewijzigd, en in plaats van "links" wordt een symmetrische reflectie van het "rechts" om de as Oy gebouwd.

De belangrijkste elementaire functies worden genoemd:

1) constante functie y = c;

2) machtsfunctie y = x α , α R ;

3) exponentiële functie y \u003d a x, a ≠ 0, a ≠1;

4) logaritmisch functie y = log a x , a > 0, a 1 ;

5) trigonometrische functies y = sin x , y = cos x , y = tg x ,

y = ctg x , y = sec x (waarbij sec x = cos 1 x ), y = cosec x (waarbij cosec x = sin 1 x );

6) inverse trigonometrische functies y \u003d arcsin x, y \u003d arccos x, y \u003d arctg x, y \u003d arcctg x.

elementaire functies zogenaamde functies verkregen uit de elementaire basisfuncties met behulp van een eindig aantal rekenkundige bewerkingen (+, − , ÷) en composities (d.w.z. de vorming van complexe functies f g ).

Voorbeeld 4.6. Een functie plotten

1) y \u003d x 2 + 6 x + 7; 2) y = −2sin 4 x .

Oplossing: 1) door het volledige vierkant te markeren, wordt de functie geconverteerd naar de vorm y = (x +3) 2 − 2, zodat de grafiek van deze functie kan worden verkregen uit de grafiek van de functie y = x 2 . Het is voldoende om eerst de parabool y \u003d x 2 drie eenheden naar links te verschuiven (we krijgen de grafiek van de functie y \u003d (x +3) 2), en dan twee eenheden naar beneden (Fig. 4.1);

	standaard-	sinusoïde						y = zonde x	vier keer langs de as		Os,
we krijgen de grafiek van de functie y \u003d sin 4 x (Fig. 4.2).
										y=sin4x
										y=zonde x

Als we de resulterende grafiek twee keer langs de Oy-as uitrekken, krijgen we de grafiek van de functie y \u003d 2sin 4 x (Fig. 4.3). Het blijft om de laatste grafiek weer te geven ten opzichte van de Ox-as. Het resultaat is de gewenste grafiek (zie Fig. 4.3).

						y=2sin4x

y=–2sin4x

Taken voor onafhankelijke oplossing

Construeer grafieken van de volgende functies, gebaseerd op de grafieken van de belangrijkste elementaire functies:

4.16. a) y \u003d x 2 -6 x +11;

4.17. a) y = −2sin(x −π ) ;

4.18. a) y = − 4 x −1 ;

4.19. a) y = log 2 (−x );

4.20. a) y = x +5;

4.21. a) y \u003d tg x;

4.22. a) y = teken x ;

4.23. a) y = x x + + 4 2 ;

y = 3 - 2 x - x 2 .

y = 2 cos 2 x .

Functie Grafiek Transformatie

In dit artikel zal ik u kennis laten maken met lineaire transformaties van functiegrafieken en u laten zien hoe u deze transformaties kunt gebruiken om een ​​functiegrafiek uit een functiegrafiek te halen.

Een lineaire transformatie van een functie is een transformatie van de functie zelf en/of zijn argument naar de vorm , evenals een transformatie die de module van het argument en/of de functies bevat.

De volgende acties veroorzaken de grootste problemen bij het plotten van grafieken met lineaire transformaties:

1. De isolatie van de basisfunctie, in feite de grafiek waarvan we transformeren.
2. Definities van de volgorde van transformaties.

En Op deze punten zullen we nader ingaan.

Laten we de functie eens nader bekijken

Het is gebaseerd op een functie. Laten we haar bellen basis functie.

Bij het plotten van een functie we maken transformaties van de grafiek van de basisfunctie.

Als we de functie zouden transformeren in dezelfde volgorde waarin de waarde werd gevonden voor een bepaalde waarde van het argument, dan

Laten we eens kijken welke soorten lineaire argument- en functietransformaties er zijn, en hoe we ze kunnen uitvoeren.

Argument transformaties.

1. f(x) f(x+b)

1. We bouwen een grafiek van een functie

2. We verschuiven de grafiek van de functie langs de OX-as met |b| eenheden

• links als b>0
• goed als b<0

Laten we de functie plotten

1. We plotten de functie

2. Schuif het 2 eenheden naar rechts:

2. f(x) f(kx)

1. We bouwen een grafiek van een functie

2. Deel de abscis van de grafiekpunten door k, laat de ordinaat van de punten ongewijzigd.

Laten we de functie plotten.

1. We plotten de functie

2. Deel alle abscis van de grafiekpunten door 2, laat de ordinaat ongewijzigd:

3. f(x) f(-x)

1. We bouwen een grafiek van een functie

2. We geven het symmetrisch om de OY-as weer.

Laten we de functie plotten.

1. We plotten de functie

2. We geven het symmetrisch om de OY-as weer:

4. f(x) f(|x|)

1. We plotten de functie

2. We wissen het deel van de grafiek dat zich links van de OY-as bevindt, het deel van de grafiek dat zich rechts van de OY-as bevindt. We vullen het symmetrisch rond de OY-as in:

De grafiek van de functie ziet er als volgt uit:

Laten we de functie plotten

1. We bouwen een functiegrafiek (dit is een functiegrafiek die 2 eenheden naar links langs de OX-as is verschoven):

2. Een deel van de grafiek bevindt zich links van de OY (x<0) стираем:

3. Het deel van de grafiek dat zich rechts van de OY-as bevindt (x>0) is symmetrisch ingevuld ten opzichte van de OY-as:

Belangrijk! De twee belangrijkste regels voor argumentconversie.

1. Alle argumenttransformaties worden uitgevoerd langs de OX-as

2. Alle transformaties van het argument worden "omgekeerd" en "in omgekeerde volgorde" uitgevoerd.

In een functie is de volgorde van argumenttransformaties bijvoorbeeld als volgt:

1. We nemen de module van x.

2. Voeg het getal 2 toe aan de modulo x.

Maar we hebben het plotten in omgekeerde volgorde gedaan:

Eerst hebben we de transformatie 2 uitgevoerd. - de grafiek met 2 eenheden naar links verschoven (dat wil zeggen, de abscis van de punten werd met 2 verminderd, alsof "vice versa")

Daarna voerden we de transformatie f(x) f(|x|) uit.

In het kort wordt de volgorde van transformaties als volgt geschreven:

Laten we het nu hebben over functie transformatie . Er worden transformaties gemaakt

1. Langs de OY-as.

2. In dezelfde volgorde waarin de acties worden uitgevoerd.

Dit zijn de transformaties:

1. f(x)f(x)+D

2. Verschuif het langs de OY-as met |D| eenheden

• omhoog als D>0
• omlaag als D<0

Laten we de functie plotten

1. We plotten de functie

2. Verplaats het langs de OY-as met 2 eenheden omhoog:

2. f(x)Af(x)

1. We plotten de functie y=f(x)

2. We vermenigvuldigen de ordinaat van alle punten van de grafiek met A, we laten de abscis ongewijzigd.

Laten we de functie plotten

1. Maak een grafiek van de functie

2. We vermenigvuldigen de ordinaat van alle punten van de grafiek met 2:

3.f(x)-f(x)

1. We plotten de functie y=f(x)

Laten we de functie plotten.

1. We bouwen een functiegrafiek.

2. We geven het symmetrisch om de OX-as weer.

4. f(x)|f(x)|

1. We plotten de functie y=f(x)

2. Het deel van de grafiek dat zich boven de OX-as bevindt, blijft ongewijzigd, het deel van de grafiek dat zich onder de OX-as bevindt, wordt symmetrisch om deze as weergegeven.

Laten we de functie plotten

1. We bouwen een functiegrafiek. Het wordt verkregen door de grafiek van de functie langs de OY-as met 2 eenheden naar beneden te verschuiven:

2. Het deel van de grafiek dat zich onder de OX-as bevindt, wordt nu symmetrisch weergegeven ten opzichte van deze as:

En de laatste transformatie, die strikt genomen geen functietransformatie kan worden genoemd, aangezien het resultaat van deze transformatie geen functie meer is:

|y|=f(x)

1. We plotten de functie y=f(x)

2. We wissen het deel van de grafiek dat zich onder de OX-as bevindt, daarna vullen we het deel van de grafiek dat zich boven de OX-as bevindt, symmetrisch rond deze as.

Laten we een grafiek van de vergelijking maken

1. We bouwen een functiegrafiek:

2. We wissen het deel van de grafiek dat zich onder de OX-as bevindt:

3. Het deel van de grafiek dat zich boven de OX-as bevindt, wordt symmetrisch om deze as ingevuld.

En tot slot raad ik je aan om de VIDEOLES te bekijken waarin ik een stapsgewijs algoritme laat zien voor het plotten van een functiegrafiek

De grafiek van deze functie ziet er als volgt uit:

Hypothese: als je de beweging van de grafiek bestudeert tijdens de vorming van de functievergelijking, zul je merken dat alle grafieken aan gemeenschappelijke wetten gehoorzamen, daarom kun je algemene wetten formuleren, ongeacht de functies, wat niet alleen de constructie van grafieken zal vergemakkelijken van verschillende functies, maar ze ook gebruiken bij het oplossen van problemen.

Doel: de beweging van grafieken van functies bestuderen:

1) De taak van het bestuderen van literatuur

2) Leer grafieken van verschillende functies te bouwen

3) Leer grafieken van lineaire functies om te zetten

4) Overweeg het gebruik van grafieken bij het oplossen van problemen

Onderzoeksobject: Grafieken van functies

Onderwerp van onderzoek: Bewegingen van grafieken van functies

Relevantie: De constructie van functiegrafieken kost in de regel veel tijd en vereist aandacht van de student, maar als u de regels kent voor het transformeren van functiegrafieken en grafieken van basisfuncties, kunt u snel en gemakkelijk functiegrafieken maken, waardoor u je niet alleen om taken uit te voeren voor het plotten van functiegrafieken, maar ook om gerelateerde problemen op te lossen (om het maximum te vinden (minimale hoogte van tijd en ontmoetingspunt))

Dit project is nuttig voor alle leerlingen van de school.

Boekbeoordeling:

De literatuur bespreekt manieren om een ​​grafiek van verschillende functies te construeren, evenals voorbeelden van de transformatie van grafieken van deze functies. Grafieken van bijna alle hoofdfuncties worden gebruikt in verschillende technische processen, wat het mogelijk maakt om het verloop van het proces duidelijker weer te geven en het resultaat te programmeren

Vaste functie. Deze functie wordt gegeven door de formule y = b, waarbij b een getal is. De grafiek van een constante functie is een rechte lijn evenwijdig aan de x-as en door het punt (0; b) op de y-as. De grafiek van de functie y \u003d 0 is de abscis.

Soorten functies 1Directe evenredigheid. Deze functie wordt gegeven door de formule y \u003d kx, waarbij de evenredigheidscoëfficiënt k ≠ 0. De directe evenredigheidsgrafiek is een rechte lijn die door de oorsprong gaat.

Lineaire functie. Zo'n functie wordt gegeven door de formule y = kx + b, waarbij k en b reële getallen zijn. De grafiek van een lineaire functie is een rechte lijn.

Lineaire functiegrafieken kunnen elkaar snijden of evenwijdig zijn.

Dus de lijnen van de grafieken van lineaire functies y \u003d k 1 x + b 1 en y \u003d k 2 x + b 2 snijden elkaar als k 1 ≠ k 2; als k 1 = k 2 , dan zijn de lijnen evenwijdig.

2 Inverse evenredigheid is een functie die wordt gegeven door de formule y \u003d k / x, waarbij k 0. K wordt de inverse evenredigheidscoëfficiënt genoemd. De inverse evenredigheidsgrafiek is een hyperbool.

De functie y \u003d x 2 wordt weergegeven door een grafiek die een parabool wordt genoemd: op het interval [-~; 0] de functie neemt af, op het interval neemt de functie toe.

De functie y \u003d x 3 neemt toe langs de gehele getallenlijn en wordt grafisch weergegeven door een kubieke parabool.

Machtsfunctie met natuurlijke exponent. Deze functie wordt gegeven door de formule y \u003d x n, waarbij n een natuurlijk getal is. Grafieken van een machtsfunctie met een natuurlijke exponent zijn afhankelijk van n. Bijvoorbeeld, als n = 1, dan is de grafiek een rechte lijn (y = x), als n = 2, dan is de grafiek een parabool, enz.

Een machtsfunctie met een negatieve integer-exponent wordt weergegeven door de formule y \u003d x -n, waarbij n een natuurlijk getal is. Deze functie is gedefinieerd voor alle x ≠ 0. De grafiek van de functie hangt ook af van de exponent n.

Machtsfunctie met een positieve fractionele exponent. Deze functie wordt weergegeven door de formule y \u003d x r, waarbij r een positieve onherleidbare breuk is. Deze functie is ook niet even of oneven.

Grafieklijn die de relatie van afhankelijke en onafhankelijke variabelen op het coördinatenvlak weergeeft. De grafiek dient om deze elementen visueel weer te geven.

Een onafhankelijke variabele is een variabele die elke waarde kan aannemen binnen het bereik van de functies (waar de gegeven functie zinvol is (kan niet worden gedeeld door nul))

Om een ​​functiegrafiek te plotten,

1) Zoek ODZ (bereik van acceptabele waarden)

2) neem enkele willekeurige waarden voor de onafhankelijke variabele

3) Zoek de waarde van de afhankelijke variabele

4) Bouw een coördinatenvlak, markeer deze punten erop

5) Verbind indien nodig hun lijnen, onderzoek de resulterende grafiek Transformatie van grafieken van elementaire functies.

Grafiekconversie

In hun pure vorm zijn de elementaire basisfuncties helaas niet zo gebruikelijk. Veel vaker heeft men te maken met elementaire functies verkregen uit elementaire basisfuncties door constanten en coëfficiënten toe te voegen. Grafieken van dergelijke functies kunnen worden gebouwd door geometrische transformaties toe te passen op de grafieken van de overeenkomstige elementaire basisfuncties (of door over te schakelen naar een nieuw coördinatensysteem). Een kwadratische functieformule is bijvoorbeeld een kwadratische paraboolformule, driemaal gecomprimeerd ten opzichte van de ordinaat-as, symmetrisch weergegeven ten opzichte van de abscis-as, verschoven tegen de richting van deze as met 2/3 eenheden en verschoven in de richting van de ordinaat as met 2 eenheden.

Laten we deze geometrische transformaties van een functiegrafiek stap voor stap begrijpen aan de hand van specifieke voorbeelden.

Met behulp van geometrische transformaties van de grafiek van de functie f (x), kan een grafiek van elke functie van de formule worden geconstrueerd, waarbij de formule de compressie- of uitzettingscoëfficiënten langs respectievelijk de oy- en ox-as is, de min tekens voor de coëfficiëntenformule en formule geven een symmetrische weergave van de grafiek ten opzichte van de coördinaatassen aan, a en b definiëren de verschuiving ten opzichte van respectievelijk de abscis en de ordinaat-assen.

Er zijn dus drie soorten geometrische transformaties van de functiegrafiek:

Het eerste type is schalen (compressie of expansie) langs de abscis en ordinaat-assen.

De noodzaak voor schaling wordt aangegeven door andere formulecoëfficiënten dan één, als het getal kleiner is dan 1, dan wordt de grafiek gecomprimeerd ten opzichte van oy en uitgerekt ten opzichte van ox, als het getal groter is dan 1, dan rekken we uit langs de ordinaat-as en krimpen langs de as van de abscis.

Het tweede type is een symmetrische (spiegel)weergave ten opzichte van de coördinaatassen.

De noodzaak van deze transformatie wordt aangegeven door de mintekens voor de coëfficiënten van de formule (in dit geval geven we de grafiek symmetrisch weer ten opzichte van de os-as) en de formule (in dit geval geven we de grafiek symmetrisch weer met ten opzichte van de y-as). Als er geen mintekens zijn, wordt deze stap overgeslagen.

DAGESTAN INSTITUUT VOOR PROFESSIONELE ONTWIKKELING

PEDAGOGISCH PERSONEEL

AFDELING FYSIEKE EN WISKUNDE ONDERWIJS EN ICT

Project

over het onderwerp:

« Constructie en p hervormingen

functie grafieken

op school wiskunde »

Rabadanova PA

wiskunde leraar

MBOU "Kochubey middelbare school"

Tarumovsky-district

2015

1. Inleiding……………………………………………………………….….3

2. Hoofdstuk l. Beoordeling van literatuur over het onderwerp van het project………………………….….5

3. Hoofdstuk II. Empirisch deel:

3.1. Basismethoden voor het converteren van functiegrafieken……….….7

3.2. Even uitzettenenvreemde functies ………….. 10

3.3. Een inverse functie plotten……………………... 11

3.4. Vervorming (compressie en spanning) van grafieken………………….12

3.5 Combinatie van overdracht, reflectie en vervorming………………......13

4. Taken voor onafhankelijke oplossing……………………..…...14

5.Conclusie…………………………………………………………………… 15

6. Conclusies…………………………………………………………..…………17

INVOERING

Transformatie van functiegrafieken is een van de fundamentele wiskundige concepten die rechtstreeks verband houden met praktische activiteiten. De grafieken weerspiegelen de variabiliteit en dynamiek van de reële wereld, de onderlinge relaties van reële objecten en fenomenen.

De functionele lijn is het basisonderwerp dat wordt behandeld in de Basis- en Unified Staatsexamens.Ook worden veel wiskundige concepten door grafische methoden beschouwd. Bijvoorbeeld omkwadratischde functie wordt geïntroduceerd en bestudeerd in nauw verband met kwadratische vergelijkingen en ongelijkheden.Hieruit volgt datleerlingen leren hoe ze grafieken van een functie kunnen bouwen en transformeren, is een van de belangrijkste taken van het wiskundeonderwijs op school.

De studie van de functie maakt het mogelijk om te vinden over:domein van definitie en reikwijdte van de functie, reikwijdteAfnemende of toenemende frequenties, asymptoten, intervallenteken constantheid, enz. Om echter een grafiek te makenkov veel functies kunnen zijngebruik een aantal methodenMaak het makkelijkerhet opbouwen van. Daarom moeten studenten de competentie hebben om grafieken te bouwen volgens methodologische schema's.

Het bovenstaande definieert:relevantie onderzoeksonderwerpen.

Studieobject is de studie van de transformatie van functionele lijngrafieken in schoolwiskunde.

Onderwerp van studie - het proces van het construeren en transformeren van functiegrafieken in een middelbare school.

Doel van de studie: educatief - bestaat uit het identificeren van een methodologisch schema voor het construeren en converteren van grafieken van een functie;ontwikkelen - ontwikkeling van abstract, algoritmisch, logisch denken, ruimtelijke verbeeldingskracht;leerzaam - opvoeding van de grafische cultuur van schoolkinderen, vorming van mentale vaardigheden.

De doelen hebben geleid tot de volgende beslissing:taken:

1. Analyseer de educatieve en methodologische over het probleem dat wordt bestudeerd.

2. Identificeer methodologische schema'stransformatie van functiegrafieken in het schoolvak wiskunde.

3. Selecteer de meest effectieve methoden en middelenconstructie en transformatie van functiegrafieken in een middelbare schoolbijdragen aan: zinvolle assimilatie van educatief materiaal; het verhogen van de cognitieve activiteit van studenten; ontwikkeling van hun creatieve vermogens.

HYPOTHESE Onderzoek: de vorming van grafische vaardigheden tijdens het bestuderen van de functies en de opvoeding van de grafische cultuur van studenten zal effectief als studenten een methodisch schema hebben voor het construeren en transformeren van functiegrafieken in een wiskundecursus op school.

HOOFDSTUK l . LITERATUUROVERZICHT OVER HET ONDERWERP VAN HET PROJECT.

Ter voorbereiding van het project hebben we de volgende literatuur bestudeerd:

Sivashinsky, I. Kh Stellingen en problemen in de algebra, elementaire functies - M., 2002. - 115 p.

Gelfand, I.M., Glagoleva, E.G., Shnol, E.E. Functies en grafieken (basistechnieken) - M., 1985. - 120 s

VZ Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Elementaire wiskunde - M., 2010 (heruitgave). - 590 p.

Kuzmin, M. K. Constructie van een grafiek van een functie - J. Wiskunde op school. - 2003. - Nr. 5. - S.61-62.

Shilov GE Hoe grafieken te bouwen? - M., 1982.

Isaak Tanatar. Geometrische transformaties van grafieken van functies - MTsNMO, 2012

BIJOpgemerkt wordt dat het vermogen om het gedrag van een functie op een bepaalde verzameling te "lezen" met behulp van een grafiek niet alleen wordt gebruikt in de loop van de wiskunde, maar ook in elke praktische menselijke activiteit waarbij hij te maken heeft met bepaalde grafische representaties van afhankelijkheden. Daarom moeten studenten in staat zijn om enkele eigenschappen ervan te bepalen uit de grafiek van een functie.

Het theoretische materiaal voor de transformatie van grafieken is strikt vermeld in. De techniek gaat vergezeld van illustraties met tekeningen, voorbeelden van verschillende complexiteit en hun oplossingen, wat het mogelijk maakt om kennis te verdiepen en complexe functies in kaart te brengen.

Vertegenwoordigt een elektronische cursus waarvan het volume en de inhoud voldoen aan de vereisten voor een wiskundecursus op de middelbare school. Het theoretische materiaal wordt ondersteund door grafische animatie-illustraties die een visuele weergave geven van het onderwerp dat wordt bestudeerd. De cursus omvat drie modules: een theoretische materiaalstudiemodule, een zelfexamenmodule en een kenniscontrolemodule.

Van , , werden methodische schema's, voorbeelden voor zelfstandig werk gebruikt voor het empirische deel van het project.

Conclusies bij hoofdstuk 1

De studie van educatieve en methodische literatuur toegestaan:

1. Identificeer methodologisch schemahet bestuderen, construeren en transformeren van grafieken van een functie in een schoolwiskundecursus.

2. Selecteer de meest effectieve methoden en middelenconstructie en transformatie van functiegrafieken in schoolwiskunde,bijdragende:

zinvolle assimilatie van educatief materiaal;

het verhogen van de cognitieve activiteit van studenten;

ontwikkeling van hun creatieve vermogens.

3. laat zien dat de functionele lijn heeft een aanzienlijke impact bij de studie van verschillende concepten in de wiskunde.

Hoofdstuk 2. EMPIRISCH DEEL

In dit hoofdstuk zullen we de belangrijkste methoden voor het transformeren van functiegrafieken beschouwen en methodologische schema's geven voor het construeren van verschillende combinaties van grafieken voor verschillende functies.

2.1. BASISTECHNIEKEN VOOR FUNCTIE GRAFIEK CONVERSIE

Translatie langs de y-as

f ( x ) f ( x )+ b .

Vooreen functie plottenja = f( x) + bspoorik:

1. maak een functiegrafiekja= f( x)

2. as verplaatsenabscis aan| b| eenheden omhoog bijb>0 of bij| b| etenneerknielen bijb < 0. Verkregen in het nieuwe systeemdinat-grafiek is de grafiek van een functieja = f( x) + b.

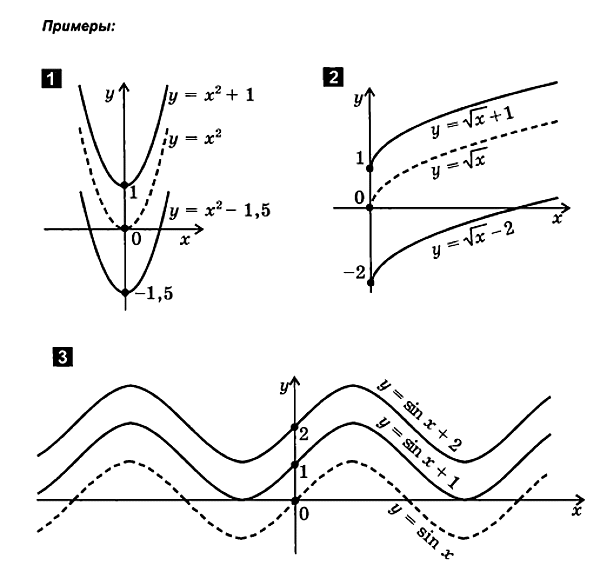
2. Overdracht langs assen abscis

f ( x ) f ( x + a ) .

ja = f( x+ a) tracerenik:

3. Een functie van de vorm plotten ja = f (- x )

f (x ) f (- x ).

Een functie plottenja = f( - x) volgt:

een functie plottenja = f( x)

reflecteer het terugten opzichte van de y-as

de resulterende grafiek isfunctie grafiekja = f( - X).

4. Een functie van de vorm plotten y= - f ( x )

f ( x ) - f ( x )

- f( x) volgt:

een functie plottenja= f( x)

spiegel het om de x-as

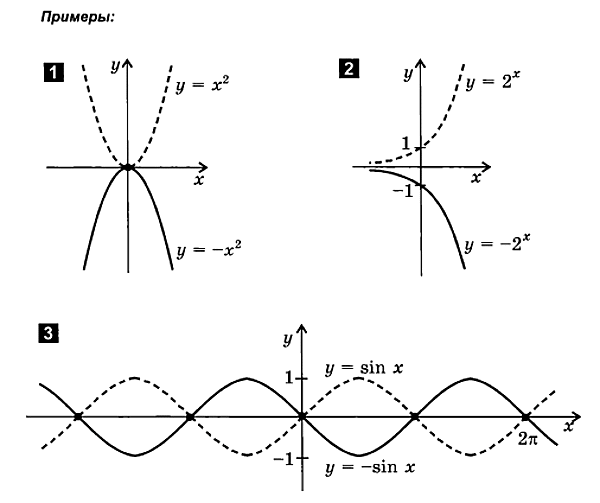
2.2. Even uitzetten en vreemde kenmerken

bij het plottenVoor even en oneven functies is het handig om de volgende eigenschappen te gebruiken:

1. Grafiek van een even functie simmetrijst ten opzichte van de y-as.

2. De grafiek van een oneven functie is symmetrisch om de oorsprong.

Om grafieken van een even en oneven functie te bouwen, volstaat het om alleen de rechtertak van de grafiek te plotten voor positieve waarden van het argument. De linkertak is symmetrisch rond de oorsprong voor een oneven functie en om de y-as voor een even functie.

Een even functie plotten ja = f ( x ) na duet:

construeer een tak van de grafiek van deze functie alleen inbereik van positieve waarden van het argument x≥0.

Otraceer deze tak om de y-as

Een oneven functie plotten ja = f ( x ) volgt:

bouw een grafiektak van deze functie alleen ingebied van positieve waarden van het argument (х≥0).

Otraceer deze tak met betrekking tot de oorsprongnaar het gebied van negatieve x-waarden.

2.3. De inverse functie plotten

Zoals reeds opgemerkt, de directe en inverse functiesdezelfde relatie tussen variabelen tonenx en y, met als enige verschil dat in de inverse functie dezevariabelen zijn van rol veranderd, wat gelijk staat aan veranderennotatie van coördinaatassen. Daarom is de grafiekde inverse functie is symmetrisch met de grafiek van de directe functieover de bissectricelenIIIcoördinaat hoeken,d.w.z. relatief rechty = x. Zo krijgen wevolgende regel.

Om de functie y = . te plotten (x) inverse van de functieja = f( x), moet worden gebouwdplanningja = f( x) en reflecteer het met betrekking tot de rechte lijn y = x.

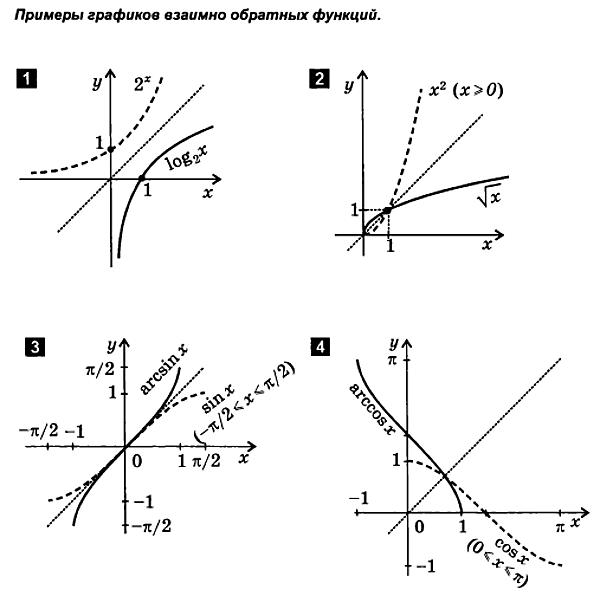
2.4. Vervorming (compressie en spanning) van grafieken

1. Compressie (expansie) van de grafiek langs de y-as

f ( x ) EEN ∙ f ( x ).

Een functie plottenja= EEN∙ f( x) volgt:

8. Compressie (expansie) van de grafiek langs de x-as

f( x)

De functie y . plotten= f( x) volgt:

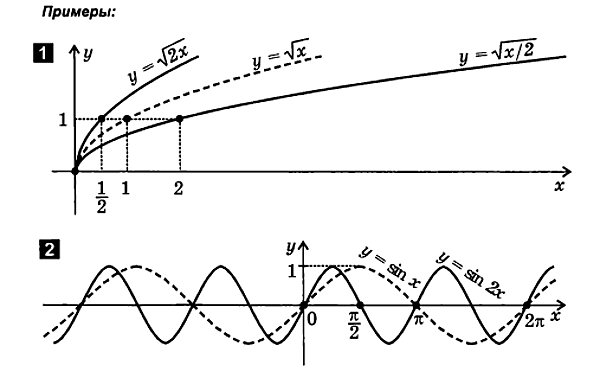
2.5. Combinatie van translatie, reflectie en vervorming

Heel vaak bij het plotten van functiegrafieken voor:verander de combinatie.

Consistente toepassing van een aantal van dergelijke houdingstechniekenmaakt het mogelijk om de constructie van een grafiek aanzienlijk te vereenvoudigen met behulp vanhardloopfunctie en verminder deze vaak uiteindelijk totconstructie van een van de eenvoudigste elementaire functiesties. Overweeg hoe, met het oog op het voorgaande, volgt:functiegrafieken maken.

Laten we er rekening mee houden dat het tijd ishet is raadzaam om het vereenvoudigingsdok in de volgende opvolger uit te voerenheid.

Pariteit of . gebruikenfunctie eigenaardigheid.

Assen overdracht.

Reflectie en vervorming.

De constructie van de grafiek wordt in omgekeerde volgorde uitgevoerd.

Voorbeeld. Een functie plotten

De constructie zal in de volgende stappen worden uitgevoerd:

1. plot de natuurlijke logaritme:

2. knijpennaar de asOY2 keer:;
3. symmetrisch weergevenover de asOY: ;
4. beweeg langs de asOSop de(!!!) naar rechts::

5. weergave symmetrisch rond de asOS: ;
6. bewegenlangs de asOY3 eenheden omhoog::

VOORBEELDEN VAN BOUW EN CONVERSIE VAN FUNCTIEGRAFIEKEN

voorbeeld 1 Een functie plotten.

Teken eerst een sinusgrafiek, de periode is gelijk aan:

functie grafiekverkregen door de grafiek te comprimerentwee keer naar de y-as. log .

Een functie plottenBij = 2 omdatX.

Een functie plottenja = zondex .

CONCLUSIE

Tijdens het werk aan het projectwerk werd verschillende educatieve en methodologische literatuur over dit onderwerp geanalyseerd. De resultaten van het onderzoek maakten het mogelijk om de meest kenmerkende positieve aspecten van het onderzoek te identificeren, constructie en transformatie van grafieken van een functie in een wiskundecursus op school

Het belangrijkste doel van het project is om de vaardigheden en capaciteiten van studenten te ontwikkelen in het lezen en tekenen van tekeningen, in de vorming van rationele methoden van onafhankelijke activiteit.

De noodzaak om het grafische onderwijs als geheel te verbeteren, wordt niet alleen ingegeven door moderne productievereisten, maar ook door de rol van grafische afbeeldingen bij de ontwikkeling van technisch denken en cognitieve vaardigheden van studenten. Het vermogen van een persoon om grafische informatie te verwerken is een van de indicatoren van zijn mentale ontwikkeling. Daarom moet grafische training een integraal onderdeel worden van de algemene onderwijsopleiding.

bevindingen

Zo is het ontwikkelde project "Constructie en transformatie van functiegrafieken", gewijd aan een van de centrale concepten van wiskunde - functionele afhankelijkheid, gericht op systematisering en uitbreiding van de kennis van studenten. De studie van specifieke methoden voor het transformeren van functiegrafieken wordt op analytische en grafische wijze uitgevoerd volgens strikte methodologische schema's. Het verzamelde materiaal kan worden gebruikt in de klas en voor zelfstudie van studenten. Een verscheidenheid aan vormen en methoden van organisatie en training kan worden gebruikt om lessen te geven.