Tekst pracy jest umieszczony bez obrazów i wzorów.
Pełna wersja pracy dostępna jest w zakładce „Pliki pracy” w formacie PDF

Wstęp

Transformacja wykresów funkcji jest jednym z podstawowych pojęć matematycznych bezpośrednio związanych z czynnościami praktycznymi. Transformacja wykresów funkcji jest po raz pierwszy spotykana w klasie algebry 9, podczas studiowania tematu „Funkcja kwadratowa”. Funkcja kwadratowa jest wprowadzana i badana w ścisłym związku z równaniami kwadratowymi i nierównościami. Również wiele pojęć matematycznych jest rozważanych metodami graficznymi, na przykład w klasach 10-11 badanie funkcji pozwala znaleźć dziedzinę definicji i zakres funkcji, obszary spadku lub wzrostu, asymptoty, interwały stałości itp. To ważne pytanie jest również kierowane do GIA. Wynika z tego, że konstruowanie i przekształcanie wykresów funkcji jest jednym z głównych zadań nauczania matematyki w szkole.

Jednak, aby wykreślić wiele funkcji, można zastosować wiele metod ułatwiających budowę. Powyższe definiuje stosowność Tematy badawcze.

Przedmiot studiów jest badaniem transformacji wykresów w matematyce szkolnej.

Przedmiot badań - proces konstruowania i przekształcania wykresów funkcji w szkole średniej.

problemowe pytanie: czy można zbudować graf nieznanej funkcji, mając umiejętność przekształcania grafów funkcji elementarnych?

Cel: wykreślanie funkcji w nieznanej sytuacji.

Zadania:

1. Przeanalizuj materiał edukacyjny dotyczący badanego problemu. 2. Identyfikować schematy przekształcania wykresów funkcji w szkolnym kursie matematyki. 3. Dobierać najbardziej efektywne metody i narzędzia do konstruowania i przekształcania wykresów funkcji. 4. Umieć zastosować tę teorię w rozwiązywaniu problemów.

Niezbędna podstawowa wiedza, umiejętności, zdolności:

Określ wartość funkcji przez wartość argumentu na różne sposoby określania funkcji;

Buduj wykresy badanych funkcji;

Opisz zachowanie i właściwości funkcji z wykresu i w najprostszych przypadkach ze wzoru znajdź największe i najmniejsze wartości z wykresu funkcji;

Opisy za pomocą funkcji o różnych zależnościach, ich reprezentacja graficzna, interpretacja wykresów.

Głównym elementem

Część teoretyczna

Jako początkowy wykres funkcji y = f(x) wybiorę funkcję kwadratową y=x 2 . Rozważę przypadki transformacji tego grafu związane ze zmianami we wzorze definiującym tę funkcję i wyciągnę wnioski dla dowolnej funkcji.

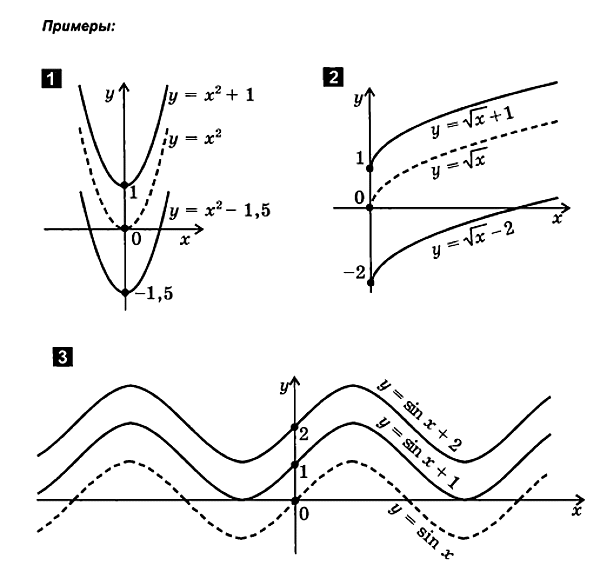
1. Funkcja y = f(x) + a

W nowej formule wartości funkcji (współrzędne punktów wykresu) są zmieniane o liczbę a, w porównaniu do „starej” wartości funkcji. Prowadzi to do równoległego przesunięcia wykresu funkcji wzdłuż osi OY:

w górę, jeśli a > 0; w dół, jeśli…< 0.

WNIOSEK

Zatem wykres funkcji y=f(x)+a otrzymujemy z wykresu funkcji y=f(x) za pomocą przesunięcia równoległego wzdłuż osi y o jednostki w górę, jeśli a > 0, oraz przez jednostki w dół, jeśli< 0.

2. Funkcja y = f(x-a),

W nowej formule wartości argumentów (odciętych punktów wykresu) są zmieniane o liczbę a w porównaniu ze „starą” wartością argumentu. Prowadzi to do równoległego przeniesienia wykresu funkcji wzdłuż osi OX: w prawo jeśli a< 0, влево, если a >0.

WNIOSEK

Tak więc wykres funkcji y= f(x - a) otrzymujemy z wykresu funkcji y=f(x) przez przesunięcie równoległe wzdłuż osi odciętej o jednostki w lewo, jeśli a > 0, io jednostki w prawo, jeśli a< 0.

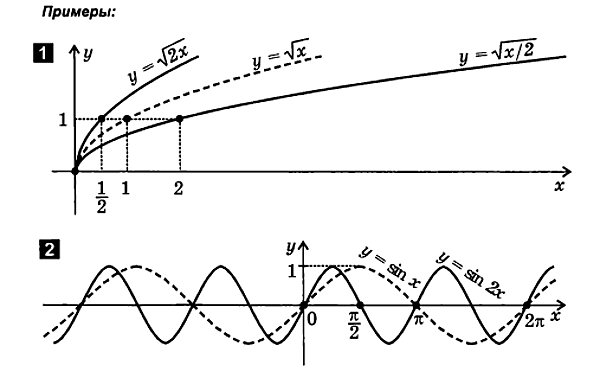
3. Funkcja y = k f(x), gdzie k > 0 i k ≠ 1

W nowej formule wartości funkcji (współrzędne punktów wykresu) zmieniają się k razy w stosunku do „starej” wartości funkcji. Prowadzi to do: 1) „rozciągnięcia” od punktu (0; 0) wzdłuż osi OY o k razy, jeżeli k > 1, 2) „ściśnięcia” do punktu (0; 0) wzdłuż osi OY o współczynnik 0, jeśli 0< k < 1.

WNIOSEK

Zatem: aby zbudować wykres funkcji y = kf(x), gdzie k > 0 i k ≠ 1, trzeba pomnożyć rzędne punktów danego wykresu funkcji y = f(x) przez k. Taka transformacja nazywana jest rozciąganiem od punktu (0; 0) wzdłuż osi OY o k razy, jeśli k > 1; skrócenie do punktu (0; 0) wzdłuż osi OY o współczynnik, jeśli 0< k < 1.

4. Funkcja y = f(kx), gdzie k > 0 i k ≠ 1

W nowej formule wartości argumentu (odcięte punkty wykresu) zmieniają się k razy w porównaniu ze „starą” wartością argumentu. Prowadzi to do: 1) „rozciągnięcia” od punktu (0; 0) wzdłuż osi OX o 1/k razy, jeśli 0< k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

WNIOSEK

I tak: aby zbudować wykres funkcji y = f(kx), gdzie k > 0 i k ≠ 1, trzeba pomnożyć odcięte punkty danego wykresu funkcji y=f(x) przez k . Taka transformacja nazywa się rozciąganiem od punktu (0; 0) wzdłuż osi OX o 1/k razy, jeśli 0< k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

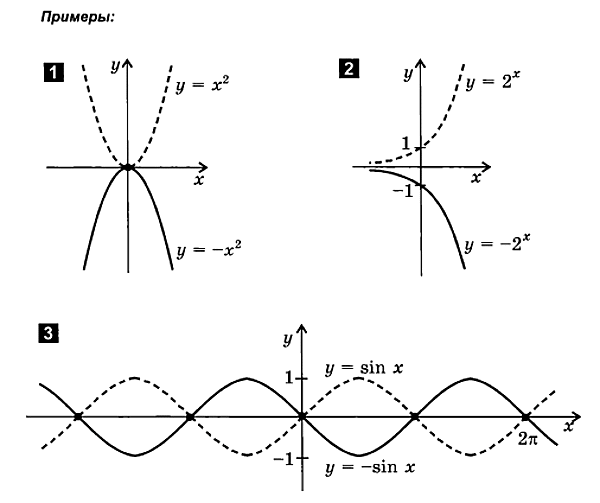
5. Funkcja y = - f (x).

W tym wzorze wartości funkcji (współrzędne punktów wykresu) są odwrócone. Ta zmiana powoduje symetryczne wyświetlanie oryginalnego wykresu funkcji wokół osi x.

WNIOSEK

Aby zbudować wykres funkcji y = - f (x), potrzebujesz wykresu funkcji y = f (x)

odbijają się symetrycznie wokół osi OX. Taka transformacja nazywana jest transformacją symetrii wokół osi OX.

6. Funkcja y = f (-x).

W tej formule wartości argumentu (odcięte punkty wykresu) są odwrócone. Ta zmiana powoduje symetryczne wyświetlanie oryginalnego wykresu funkcji względem osi OY.

Przykład dla funkcji y \u003d - x² ta transformacja nie jest zauważalna, ponieważ ta funkcja jest parzysta, a wykres nie zmienia się po transformacji. Ta transformacja jest widoczna, gdy funkcja jest nieparzysta i gdy ani parzysta, ani nieparzysta.

7. Funkcja y = |f(x)|.

W nowej formule wartości funkcji (współrzędne punktów wykresu) znajdują się pod znakiem modułu. Prowadzi to do zaniku części wykresu pierwotnej funkcji o rzędnych ujemnych (czyli znajdujących się w dolnej półpłaszczyźnie względem osi Wół) i symetrycznego wyświetlania tych części względem osi Wół.

8. Funkcja y= f (|x|).

W nowej formule wartości argumentów (odcięte punkty wykresu) znajdują się pod znakiem modułu. Prowadzi to do zaniku części wykresu pierwotnej funkcji z odciętymi ujemnymi (czyli tych znajdujących się w lewej półpłaszczyźnie względem osi OY) i zastąpienia ich fragmentami oryginalnego wykresu, które są symetryczne względem OY oś.

Część praktyczna

Rozważ kilka przykładów zastosowania powyższej teorii.

PRZYKŁAD 1.

Decyzja. Przekształćmy tę formułę:

1) Zbudujmy wykres funkcji

PRZYKŁAD 2.

Wykreśl funkcję podaną przez wzór

Decyzja. Przekształcamy tę formułę, podświetlając kwadrat dwumianu w tym trójmianie kwadratowym:

1) Zbudujmy wykres funkcji

2) Wykonaj równoległy transfer skonstruowanego grafu do wektora

PRZYKŁAD 3.

ZADANIE Z UŻYTKOWANIA Wykreślanie funkcji odcinkowej

Wykres funkcji Wykres funkcji y=|2(x-3)2-2|; jeden

Która z tych funkcji ma odwrotność? Dla takich funkcji znajdź funkcje odwrotne:

4.12. a)	y=x;					b) y = 6-3x;
d) y =						e) y \u003d 2 x 3 +5;
4.13. a)	y = 4x-5 ;						y \u003d 9 - 2 x - x 2;
	y = znak x ;						y=1 + lg(x + 2) ;

	y = 2 x 2 +1 ;
			x − 2
						o x< 0
c) y =		−x
						dla x ≥ 0

Dowiedz się, które z tych funkcji są monotoniczne, które są ściśle monotoniczne, a które są ograniczone:

4.14. a)

f(x) = c, cR;

b) f (x) \u003d cos 2 x;

c) f (x) \u003d arctg x;

d) f (x) \u003d e 2 x;

e) f (x) \u003d -x 2 + 2 x;

e) f(x) =

2x+5

y = ctg7 x .

4.15. a)

f(x) = 3− x

b) f(x) =

f(x)=

x + 3

x+6

x< 0,

3x+5

d) f (x) \u003d 3 x 3 - x;

− 10 godz

f(x)=

e) f(x) =

x 2 godz

x ≥ 0;

x+1

f(x) = tg(sinx).

4.2. funkcje podstawowe. Transformacja wykresu funkcji

Przypomnijmy, że wykres funkcji f (x) w kartezjańskim prostokątnym układzie współrzędnych Oxy jest zbiorem wszystkich punktów na płaszczyźnie o współrzędnych (x, f (x)).

Często wykres funkcji y \u003d f (x) można zbudować za pomocą przekształceń (przesunięcie, rozciąganie) wykresu jakiejś znanej już funkcji.

W szczególności z wykresu funkcji y \u003d f (x) otrzymuje się wykres funkcji:

1) y \u003d f (x) + a - przesunięcie wzdłuż osi Oy o jednostki (w górę, jeśli a > 0, i w dół, jeśli a< 0 ;

2) y \u003d f (x − b) - przesunięcie wzdłuż osi Wół o b jednostek (w prawo, jeśli b > 0,

i po lewej jeśli b< 0 ;

3) y \u003d kf (x) - przez rozciąganie wzdłuż osi Oy k razy;

4) y \u003d f (mx) - kompresja wzdłuż osi Wół przez m razy;

5) y \u003d - f (x) - symetryczne odbicie wokół osi Ox;

6) y \u003d f (−x) - symetryczne odbicie wokół osi Oy;

7) y \u003d f (x), w następujący sposób: część wykresu znajdująca się nie

poniżej osi Wół pozostaje bez zmian, a „dolna” część wykresu jest odbita symetrycznie względem osi Wół;

8) y = f (x ) , jak następuje: prawa strona wykresu (dla x ≥ 0 )

pozostaje bez zmian, a zamiast „lewego” zbudowane jest symetryczne odbicie „prawego” wokół osi Oy.

Główne funkcje podstawowe to:

1) funkcja stała y = c;

2) funkcja potęgowa y = x α , α R ;

3) funkcja wykładnicza y \u003d a x, a 0, a ≠1;

4) logarytmiczny funkcja y = log a x , a > 0, a ≠ 1 ;

5) trygonometryczny funkcje y = sin x , y = cos x , y = tg x ,

y = ctgx, y = sec x (gdzie sec x = cos 1 x ), y = cosec x (gdzie cosec x = sin 1 x );

6) odwrotne funkcje trygonometryczne y \u003d arcsin x, y \u003d arccos x, y \u003d arctg x, y \u003d arcctg x.

podstawowe funkcje zwane funkcjami uzyskanymi z podstawowych funkcji elementarnych za pomocą skończonej liczby działań arytmetycznych (+, − , ÷) i złożeń (tj. tworzenie funkcji zespolonych f g ).

Przykład 4.6. Wykreśl funkcję

1) y \u003d x 2 + 6 x + 7; 2) y = -2sin 4 x .

Rozwiązanie: 1) przez podświetlenie pełnego kwadratu funkcja jest konwertowana do postaci y = (x +3) 2 − 2, czyli wykres tej funkcji można otrzymać z wykresu funkcji y = x 2 . Wystarczy najpierw przesunąć parabolę y \u003d x 2 o trzy jednostki w lewo (otrzymujemy wykres funkcji y \u003d (x +3) 2), a następnie dwie jednostki w dół (ryc. 4.1);

	standard	sinusoida						y = grzech x	cztery razy wzdłuż osi		Wół,
otrzymujemy wykres funkcji y \u003d sin 4 x (ryc. 4.2).
										y=sin4x
										y=grzech x

Rozciągając wynikowy wykres dwukrotnie wzdłuż osi Oy, otrzymujemy wykres funkcji y \u003d 2sin 4 x (ryc. 4.3). Pozostaje odzwierciedlenie ostatniego wykresu względem osi Wół. Wynikiem będzie pożądany wykres (patrz rys. 4.3).

						y=2sin4x

y=–2sin4x

Zadania do samodzielnego rozwiązania

Skonstruuj wykresy następujących funkcji na podstawie wykresów głównych funkcji elementarnych:

4.16. a) y \u003d x 2 -6 x +11;

4.17. a) y = -2sin(x-π);

4.18. a) y = -4 x -1 ;

4.19. a) y = log 2 (-x );

4.20. a) y = x +5 ;

4.21. a) y \u003d tg x;

4.22. a) y = znak x ;

4.23. a) y = x x + + 4 2 ;

y = 3 - 2 x - x 2 .

y = 2 cos 2 x .

Transformacja wykresu funkcji

W tym artykule przedstawię przekształcenia liniowe wykresów funkcji i pokażę, jak wykorzystać te przekształcenia do uzyskania wykresu funkcji z wykresu funkcji.

Transformacja liniowa funkcji to transformacja samej funkcji i/lub jej argumentu do postaci , a także przekształcenie zawierające moduł argumentu i/lub funkcji.

Największe trudności w kreśleniu wykresów z wykorzystaniem przekształceń liniowych powodują następujące czynności:

1. Izolacja funkcji bazowej, w rzeczywistości wykres, którego transformujemy.
2. Definicje porządku przekształceń.

I Właśnie w tych punktach omówimy bardziej szczegółowo.

Przyjrzyjmy się bliżej funkcji

Opiera się na funkcji. Zadzwońmy do niej podstawowa funkcja.

Podczas wykreślania funkcji dokonujemy przekształceń wykresu funkcji bazowej .

Gdybyśmy mieli przekształcić funkcję w tej samej kolejności, w jakiej ustalono jej wartość dla określonej wartości argumentu, to

Zastanówmy się, jakie typy liniowych przekształceń argumentów i funkcji istnieją i jak je wykonać.

Przekształcenia argumentów.

1. f(x) f(x+b)

1. Budujemy wykres funkcji

2. Przesuwamy wykres funkcji wzdłuż osi OX o |b| jednostki

• lewo, jeśli b>0
• dobrze, jeśli b<0

Wykreślmy funkcję

1. Wykreślamy funkcję

2. Przesuń go o 2 jednostki w prawo:

2. f(x) f(kx)

1. Budujemy wykres funkcji

2. Podziel odcięte punkty wykresu przez k, rzędne punktów pozostaw bez zmian.

Wykreślmy funkcję.

1. Wykreślamy funkcję

2. Podziel wszystkie odcięte punkty wykresu przez 2, rzędne pozostaw bez zmian:

3. f(x) f(-x)

1. Budujemy wykres funkcji

2. Wyświetlamy go symetrycznie wokół osi OY.

Wykreślmy funkcję.

1. Wykreślamy funkcję

2. Wyświetlamy go symetrycznie wokół osi OY:

4. f(x) f(|x|)

1. Wykreślamy funkcję

2. Wymazujemy część wykresu znajdującą się na lewo od osi OY, część wykresu znajdującą się na prawo od osi OY Uzupełniamy go symetrycznie względem osi OY:

Wykres funkcji wygląda tak:

Wykreślmy funkcję

1. Budujemy wykres funkcji (jest to wykres funkcji przesunięty wzdłuż osi OX o 2 jednostki w lewo):

2. Część wykresu znajdująca się po lewej stronie OY (x<0) стираем:

3. Część wykresu znajdująca się na prawo od osi OY (x>0) jest uzupełniana symetrycznie względem osi OY:

Ważny! Dwie główne zasady konwersji argumentów.

1. Wszystkie przekształcenia argumentów wykonywane są wzdłuż osi OX

2. Wszystkie przekształcenia argumentu wykonywane są „odwrotnie” i „w odwrotnej kolejności”.

Na przykład w funkcji sekwencja przekształceń argumentów jest następująca:

1. Bierzemy moduł z x.

2. Dodaj liczbę 2 do modulo x.

Ale kreśliliśmy w odwrotnej kolejności:

Najpierw wykonaliśmy transformację 2. - przesunęliśmy wykres o 2 jednostki w lewo (czyli odcięte punkty zostały zmniejszone o 2, jakby „na odwrót”)

Następnie wykonaliśmy transformację f(x) f(|x|).

W skrócie sekwencja przekształceń jest napisana w następujący sposób:

Teraz porozmawiajmy o transformacja funkcji . Dokonują się przemiany

1. Wzdłuż osi OY.

2. W tej samej kolejności, w jakiej wykonywane są akcje.

Oto przekształcenia:

1. f(x)f(x)+D

2. Przesuń go wzdłuż osi OY o |D| jednostki

• w górę, jeśli D>0
• w dół, jeśli D<0

Wykreślmy funkcję

1. Wykreślamy funkcję

2. Przesuń go wzdłuż osi OY o 2 jednostki w górę:

2. f(x)Af(x)

1. Wykreślamy funkcję y=f(x)

2. Mnożymy rzędne wszystkich punktów wykresu przez A, odcięte pozostawiamy bez zmian.

Wykreślmy funkcję

1. Wykres funkcji

2. Mnożymy rzędne wszystkich punktów wykresu przez 2:

3.f(x)-f(x)

1. Wykreślamy funkcję y=f(x)

Wykreślmy funkcję.

1. Budujemy wykres funkcji.

2. Wyświetlamy go symetrycznie wokół osi OX.

4. f(x)|f(x)|

1. Wykreślamy funkcję y=f(x)

2. Część wykresu znajdująca się nad osią OX pozostaje niezmieniona, część wykresu znajdująca się poniżej osi OX jest wyświetlana symetrycznie względem tej osi.

Wykreślmy funkcję

1. Budujemy wykres funkcji. Uzyskuje się go przesuwając wykres funkcji wzdłuż osi OY o 2 jednostki w dół:

2. Teraz część wykresu znajdująca się poniżej osi OX będzie wyświetlana symetrycznie względem tej osi:

I ostatnia transformacja, której ściśle mówiąc nie można nazwać transformacją funkcji, ponieważ wynikiem tej transformacji nie jest już funkcja:

|y|=f(x)

1. Wykreślamy funkcję y=f(x)

2. Wymazujemy część wykresu znajdującą się poniżej osi OX, następnie uzupełniamy część wykresu znajdującą się powyżej osi OX symetrycznie względem tej osi.

Zbudujmy wykres równania

1. Budujemy wykres funkcji:

2. Usuwamy część wykresu znajdującą się poniżej osi OX:

3. Część wykresu znajdująca się nad osią OX jest uzupełniona symetrycznie względem tej osi.

I na koniec proponuję obejrzeć LEKCJĘ WIDEO, w której pokazuję krok po kroku algorytm wykreślania wykresu funkcji

Wykres tej funkcji wygląda tak:

Hipoteza: Jeśli przestudiujesz ruch wykresu podczas tworzenia równania funkcji, zauważysz, że wszystkie wykresy są zgodne ze wspólnymi prawami, dlatego możesz formułować ogólne prawa niezależnie od funkcji, co nie tylko ułatwi konstruowanie wykresów różnych funkcji, ale także wykorzystywać je w rozwiązywaniu problemów.

Cel: Badanie ruchu wykresów funkcji:

1) Zadanie studiowania literatury

2) Naucz się budować wykresy różnych funkcji

3) Naucz się konwertować wykresy funkcji liniowych

4) Rozważ użycie wykresów w rozwiązywaniu problemów

Przedmiot badań: Wykresy funkcji

Przedmiot badań: Ruchy wykresów funkcji

Trafność: Budowa wykresów funkcyjnych z reguły zajmuje dużo czasu i wymaga uwagi ucznia, ale znając zasady przekształcania wykresów funkcyjnych oraz wykresów funkcji podstawowych można szybko i łatwo zbudować wykresy funkcyjne, które pozwolą nie tylko wykonujesz zadania związane z kreśleniem wykresów funkcji, ale także rozwiązywasz powiązane problemy (aby znaleźć maksimum (minimalną wysokość czasu i punkt spotkania))

Ten projekt jest przydatny dla wszystkich uczniów szkoły.

Przegląd literatury:

W literaturze omawiane są sposoby konstruowania wykresów różnych funkcji, a także przykłady przekształceń wykresów tych funkcji. Wykresy prawie wszystkich głównych funkcji są wykorzystywane w różnych procesach technicznych, co pozwala na bardziej przejrzyste przedstawienie przebiegu procesu i zaprogramowanie wyniku

Funkcja stała. Ta funkcja jest wyrażona wzorem y = b, gdzie b jest pewną liczbą. Wykres funkcji stałej jest linią prostą równoległą do osi x i przechodzącą przez punkt (0; b) na osi y. Wykres funkcji y \u003d 0 to oś odciętej.

Rodzaje funkcji 1Proporcjonalność bezpośrednia. Ta funkcja jest wyrażona wzorem y \u003d kx, gdzie współczynnik proporcjonalności k ≠ 0. Wykres bezpośredniej proporcjonalności jest linią prostą przechodzącą przez początek.

Funkcja liniowa. Taką funkcję wyraża wzór y = kx + b, gdzie k i b są liczbami rzeczywistymi. Wykres funkcji liniowej jest linią prostą.

Wykresy funkcji liniowych mogą się przecinać lub być równoległe.

Tak więc linie wykresów funkcji liniowych y \u003d k 1 x + b 1 i y \u003d k 2 x + b 2 przecinają się, jeśli k 1 ≠ k 2; jeśli k 1 = k 2 , to linie są równoległe.

2 Odwrotna proporcjonalność to funkcja wyrażona wzorem y \u003d k / x, gdzie k ≠ 0. K nazywa się współczynnikiem odwrotnej proporcjonalności. Wykres odwrotnej proporcjonalności to hiperbola.

Funkcja y \u003d x 2 jest reprezentowana przez wykres zwany parabolą: w przedziale [-~; 0] funkcja maleje, w przedziale funkcji rośnie.

Funkcja y \u003d x 3 rośnie wzdłuż całej osi liczbowej i jest graficznie reprezentowana przez sześcienną parabolę.

Funkcja potęgowa z wykładnikiem naturalnym. Ta funkcja jest wyrażona wzorem y \u003d x n, gdzie n jest liczbą naturalną. Wykresy funkcji potęgowej z wykładnikiem naturalnym zależą od n. Na przykład, jeśli n = 1, to wykres będzie linią prostą (y = x), jeśli n = 2, to wykres będzie parabolą itd.

Funkcja potęgowa z ujemnym wykładnikiem całkowitym jest reprezentowana przez wzór y \u003d x -n, gdzie n jest liczbą naturalną. Ta funkcja jest zdefiniowana dla wszystkich x ≠ 0. Wykres funkcji zależy również od wykładnika n.

Funkcja potęgowa z dodatnim wykładnikiem ułamkowym. Ta funkcja jest reprezentowana przez wzór y \u003d x r, gdzie r jest dodatnim ułamkiem nieredukowalnym. Ta funkcja nie jest również ani parzysta, ani nieparzysta.

Linia wykresu wyświetlająca relacje zmiennych zależnych i niezależnych na płaszczyźnie współrzędnych. Wykres służy do wizualnego przedstawienia tych elementów.

Zmienna niezależna to zmienna, która może przyjąć dowolną wartość w zakresie funkcji (gdzie dana funkcja ma sens (nie można jej podzielić przez zero))

Aby wykreślić wykres funkcji,

1) Znajdź ODZ (zakres dopuszczalnych wartości)

2) weź kilka dowolnych wartości dla zmiennej niezależnej

3) Znajdź wartość zmiennej zależnej

4) Zbuduj płaszczyznę współrzędnych, zaznacz na niej te punkty

5) Połącz ich linie jeśli to konieczne, zbadaj wynikowy wykres Transformacja wykresów funkcji elementarnych.

Konwersja wykresu

W czystej postaci podstawowe funkcje elementarne nie są niestety tak powszechne. Znacznie częściej mamy do czynienia z funkcjami elementarnymi uzyskanymi z podstawowych funkcji elementarnych przez dodanie stałych i współczynników. Wykresy takich funkcji można zbudować, stosując przekształcenia geometryczne do wykresów odpowiednich podstawowych funkcji elementarnych (lub przełączając się na nowy układ współrzędnych). Na przykład wzór funkcji kwadratowej to wzór paraboli kwadratowej, skompresowany trzykrotnie względem osi rzędnych, wyświetlany symetrycznie względem osi odciętej, przesunięty w stosunku do kierunku tej osi o 2/3 jednostki i przesunięty wzdłuż kierunku rzędnej oś o 2 jednostki.

Zrozummy te geometryczne przekształcenia wykresu funkcji krok po kroku na konkretnych przykładach.

Za pomocą przekształceń geometrycznych wykresu funkcji f (x) można skonstruować wykres dowolnej funkcji o wzorze postaci, w którym formułą są współczynniki kompresji lub rozszerzania odpowiednio wzdłuż osi oy i ox, minus znaki przed wzorem i wzorem współczynników oznaczają symetryczne wyświetlanie wykresu względem osi współrzędnych , a i b określają przesunięcie odpowiednio względem osi odciętych i rzędnych.

Istnieją zatem trzy rodzaje przekształceń geometrycznych grafu funkcji:

Pierwszy typ to skalowanie (ściskanie lub rozszerzanie) wzdłuż osi odciętych i rzędnych.

Na potrzebę skalowania wskazują współczynniki wzoru inne niż jeden, jeśli liczba jest mniejsza niż 1, to wykres jest kompresowany względem oy i rozciągany względem ox, jeśli liczba jest większa niż 1, to rozciągamy wzdłuż osi rzędnych i kurczyć się wzdłuż osi odciętej.

Drugi typ to wyświetlanie symetryczne (lustrzane) względem osi współrzędnych.

O potrzebie tego przekształcenia świadczą znaki minusa przed współczynnikami wzoru (w tym przypadku wykres wyświetlamy symetrycznie względem osi wół) i formuły (w tym przypadku wyświetlamy wykres symetrycznie z względem osi y). Jeśli nie ma znaków minus, ten krok jest pomijany.

DAGESTAN INSTYTUT ROZWOJU ZAWODOWEGO

PERSONEL PEDAGOGICZNY

KATEDRA EDUKACJI FIZYCZNEJ I MATEMATYCZNEJ ORAZ ICT

Projekt

na temat:

« Budowa i p reformy

wykresy funkcji

w matematyce szkolnej »

Rabadanova P.A.

nauczyciel matematyki

MBOU "Szkoła średnia Koczubej"

Rejon Tarumowski

2015

1. Wstęp……………………………………………………………….….3

2. Rozdział I. Przegląd literatury na temat projektu……………………………….….5

3. Rozdział II. Część empiryczna:

3.1. Podstawowe metody konwersji wykresów funkcyjnych……….….7

3.2. Wykreślanie wydarzeniaorazfunkcje nieparzyste…………….. 10

3.3. Wykreślanie funkcji odwrotnej………………………... 11

3.4. Odkształcenie (ściskanie i rozciąganie) wykresów………………….12

3.5 Kombinacja przenoszenia, odbicia i odkształcenia ………………………13

4. Zadania do samodzielnego rozwiązania………………………..…...14

5.Wniosek………………………………………………………………………15

6. Wnioski………………………………………………………………..………17

WPROWADZENIE

Transformacja wykresów funkcji jest jednym z podstawowych pojęć matematycznych bezpośrednio związanych z czynnościami praktycznymi. Wykresy odzwierciedlają zmienność i dynamizm świata rzeczywistego, wzajemne relacje rzeczywistych obiektów i zjawisk.

Linia funkcjonalna to podstawowy temat poruszany w egzaminach Basic i Unified State Examinations.Ponadto wiele pojęć matematycznych jest rozważanych metodami graficznymi. Na przykład, abykwadratowyfunkcja jest wprowadzana i badana w ścisłym związku z równaniami kwadratowymi i nierównościami.Stąd wynika, żenauczenie uczniów budowania i przekształcania wykresów funkcji jest jednym z głównych zadań nauczania matematyki w szkole.

Badanie funkcji pozwala znaleźć informacje odziedzina definicji i zakres funkcji, zakresZmniejszanie lub zwiększanie częstości, asymptoty, interwałyznak stałości itp. Jednak aby zbudować wykreskov może być wiele funkcjikorzystać z wielu metodUłatwić tobudynek. Dlatego studenci powinni posiadać umiejętność budowania wykresów według schematów metodologicznych.

Powyższe definiujestosowność Tematy badawcze.

Przedmiot studiów jest badaniem transformacji funkcjonalnych wykresów liniowych w matematyce szkolnej.

Przedmiot badań - proces konstruowania i przekształcania wykresów funkcji w szkole średniej.

Cel badania: edukacyjny - polega na określeniu schematu metodologicznego konstruowania i przekształcania wykresów funkcji;rozwój - rozwój myślenia abstrakcyjnego, algorytmicznego, logicznego, wyobraźni przestrzennej;edukacyjny - edukacja kultury graficznej uczniów, kształtowanie umiejętności umysłowych.

Cele doprowadziły do ​​​​decyzji następującychzadania:

1. Dokonać analizy edukacyjnej i metodycznej na badanym problemie.

2. Zidentyfikuj schematy metodologicznetransformacja wykresów funkcji w szkolnym toku matematyki.

3. Wybierz najskuteczniejsze metody i środkikonstrukcja i transformacja wykresów funkcji w szkole średniejprzyczynianie się do: sensownego przyswajania materiałów edukacyjnych; zwiększenie aktywności poznawczej uczniów; rozwój ich zdolności twórczych.

HIPOTEZA Badania: kształtowanie umiejętności graficznych w procesie studiowania funkcji i edukacji kultury graficznej studentów będzie skuteczne, jeśli uczniowie mają schemat metodyczny konstruowania i przekształcania wykresów funkcji na szkolnym kursie matematyki.

ROZDZIAŁ I . PRZEGLĄD LITERATURY NA TEMAT PROJEKTU.

W ramach przygotowań do projektu przestudiowaliśmy następującą literaturę:

Sivashinsky, I. Kh. Twierdzenia i problemy w algebrze, funkcje elementarne - M., 2002. - 115 s.

Gelfand, I.M., Glagoleva, E.G., Shnol, E.E. Funkcje i wykresy (podstawowe techniki) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryżkow, MI Scanavi. Matematyka elementarna - M., 2010 (reedycja). - 590 pkt.

Kuzmin, M. K. Konstrukcja wykresu funkcji - J. Matematyka w szkole. - 2003 r. - nr 5. - S. 61-62.

Szyłow G.E. Jak budować wykresy? - M., 1982.

Izaak Tanatar. Transformacje geometryczne wykresów funkcji - MTsNMO, 2012

WNależy zauważyć, że umiejętność „odczytania” zachowania funkcji na określonym zbiorze za pomocą wykresu jest wykorzystywana nie tylko w toku matematyki, ale także w każdej praktycznej działalności człowieka, w której ma on do czynienia z pewnymi graficznymi reprezentacjami zależności. Dlatego studenci powinni umieć określić niektóre jej własności z wykresu funkcji.

Materiał teoretyczny do transformacji wykresów jest ściśle określony w. Technikę uzupełniają ilustracje z rysunkami, przykładami o różnym stopniu złożoności i ich rozwiązaniami, co pozwala pogłębić wiedzę i kreślić złożone funkcje.

Reprezentuje elektroniczny kurs szkoleniowy, którego objętość i treść spełniają wymagania kursu matematyki w szkole średniej. Materiał teoretyczny wsparty jest graficznymi ilustracjami animacyjnymi, które dają wizualną reprezentację badanego tematu. Kurs obejmuje trzy moduły: moduł nauki materiału teoretycznego, moduł samokontroli oraz moduł kontroli wiedzy.

Z , , schematy metodyczne wykresów, przykłady do samodzielnej pracy zostały wykorzystane do części empirycznej projektu.

Wnioski do rozdziału 1

Badanie literatury edukacyjnej i metodycznej pozwoliło:

1. Zidentyfikuj schemat metodologicznystudiowanie, konstruowanie i przekształcanie wykresów funkcji w szkolnym kursie matematyki.

2. Wybierz najskuteczniejsze metody i środkikonstrukcja i transformacja wykresów funkcji w matematyce szkolnej,przyczyniając się:

sensowna asymilacja materiałów edukacyjnych;

zwiększenie aktywności poznawczej uczniów;

rozwój ich zdolności twórczych.

3. pokaż, że linia funkcjonalna ma znaczący wpływ na badanie różnych pojęć w matematyce.

Rozdział 2. CZĘŚĆ EMPIRYCZNA

W tym rozdziale rozważymy główne metody przekształcania grafów funkcji i przedstawimy schematy metodologiczne konstruowania różnych kombinacji grafów dla różnych funkcji.

2.1. PODSTAWOWE TECHNIKI KONWERSJI WYKRESÓW FUNKCJI

Przesunięcie wzdłuż osi y

F ( x ) F ( x )+ b .

Dowykreślanie funkcjitak = F( x) + bnamierzaćje:

1. zbuduj wykres funkcjitak= F( x)

2. przesuń ośodcięta włączona| b| jednostki się ob>0 lub w| b| jeśćpadać na twarzb < 0. Uzyskane w nowym systemiedinat graph to wykres funkcjitak = F( x) + b.

2. Przeniesienie przed siebie osie odcięta

F ( x ) F ( x + a ) .

tak = F( x+ a) namierzaćje:

3. Wykreślanie funkcji formy tak = F (- x )

F (x ) F (- x ).

Aby wykreślić funkcjętak = F( - x) następuje:

wykreśl funkcjętak = F( x)

odbij to z powrotemwzględem osi y

wynikowy wykres towykres funkcjitak = F( - X).

4. Wykreślanie funkcji formy y= - F ( x )

F ( x ) - F ( x )

- F( x) następuje:

wykreśl funkcjętak= F( x)

odzwierciedlić to w osi x

2.2. Wykreślanie wydarzenia oraz dziwne cechy

Podczas kreśleniaW przypadku funkcji parzystych i nieparzystych wygodnie jest użyć następujących właściwości:

1. Wykres simmet funkcji parzystejryż w stosunku do osi y.

2. Wykres funkcji nieparzystej jest symetryczny względem początku.

Aby zbudować wykresy funkcji parzystej i nieparzystej wystarczy wykreślić tylko prawą gałąź wykresu dla dodatnich wartości argumentu. Lewa gałąź jest zakończona symetrycznie wokół początku funkcji nieparzystej i wokół osi y funkcji parzystej.

Aby wykreślić funkcję parzystą tak = F ( x ) po duet:

skonstruuj gałąź wykresu tej funkcji tylko wzakres dodatnich wartości argumentu x≥0.

Oprześledź tę gałąź wokół osi y

Aby wykreślić nieparzystą funkcję tak = F ( x ) następuje:

zbuduj gałąź grafu tej funkcji tylko wobszar dodatnich wartości argumentu (х≥0).

Oprześledź tę gałąź w odniesieniu do pochodzeniado obszaru ujemnych wartości x.

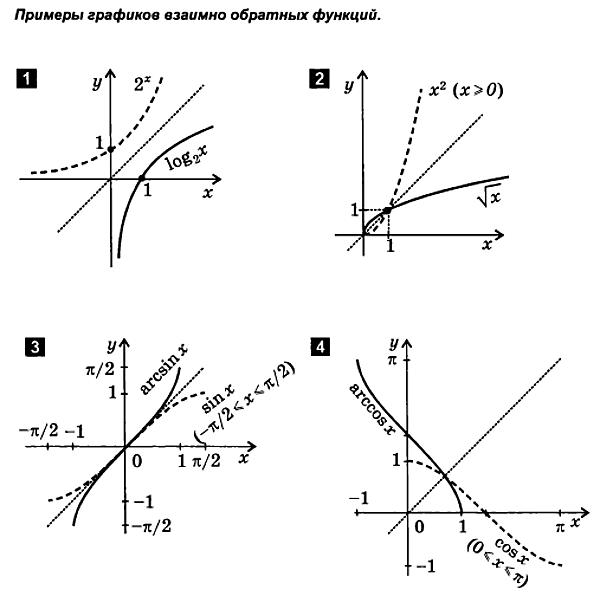
2.3. Wykreślanie funkcji odwrotnej

Jak już wspomniano, funkcja prosta i odwrotnapokaż tę samą zależność między zmiennymix i y, z tą tylko różnicą, że w funkcji odwrotnej tezmienne zmieniły role, co jest równoznaczne ze zmianązapis osi współrzędnych. Dlatego wykresfunkcja odwrotna jest symetryczna do wykresu funkcji prostejo dwusiecznejIorazIIIkąty współrzędnych,czyli stosunkowo prostey = x. W ten sposób otrzymujemynastępna zasada.

Aby wykreślić funkcję y = (x) odwrotność funkcjitak = F( x), powinien być zbudowanyharmonogramtak = F( x) i odzwierciedlić ją w odniesieniu do linii prostej y = x.

2.4. Odkształcenie (ściskanie i rozciąganie) wykresów

1. Kompresja (rozszerzenie) wykresu wzdłuż osi y

F ( x ) A ∙ F ( x ).

Aby wykreślić funkcjętak= A∙ F( x) następuje:

8. Kompresja (rozszerzenie) wykresu wzdłuż osi x

F( x)

Aby wykreślić funkcję y= F( x) następuje:

2.5. Połączenie translacji, odbicia i deformacji

Bardzo często podczas kreślenia wykresów funkcji dlazmień kombinację.

Konsekwentne stosowanie wielu takich technik postawypozwala znacznie uprościć budowę wykresu za pomocądziała funkcja i często zmniejsza ją w końcu dobudowa jednej z najprostszych funkcji elementarnychcji. Zastanów się, jak w świetle powyższego wynika to:budowanie wykresów funkcji.

Zwróćmy uwagę, że nadszedł czaswskazane jest przeprowadzenie doku uproszczenia w kolejnym następcyness.

Używając parzystości lubdziwność funkcji.

Przeniesienie osi.

Odbicie i deformacja.

Konstrukcję wykresu wykonuje się w odwrotnej kolejności.

Przykład. Wykreśl funkcję

Budowa będzie realizowana w następujących krokach:

1. wykreśl logarytm naturalny:

2. ściśnijdo osiOY2 razy:;
3. wyświetlaj symetryczniewokół osiOY: ;
4. poruszaj się wzdłuż osiWÓŁna(!!!) w prawo::

5. wyświetlaj symetrycznie wokół osiWÓŁ: ;
6. ruchwzdłuż osiOY3 jednostki w górę::

PRZYKŁADY KONSTRUKCJI I KONWERSJI WYKRESÓW FUNKCJI

Przykład 1 Wykreśl funkcję.

Najpierw narysuj wykres sinusoidalny, którego okres jest równy:

wykres funkcjiuzyskany przez kompresję wykresudwukrotnie do osi y. dziennik .

Wykreśl funkcjęw = 2 sałataX.

Wykreśl funkcjętak = grzechx .

WNIOSEK

W trakcie prac nad pracami projektowymi przeanalizowano różnorodną literaturę edukacyjną i metodologiczną dotyczącą tego zagadnienia. Wyniki badania pozwoliły na zidentyfikowanie najbardziej charakterystycznych pozytywnych aspektów badania, konstrukcja i transformacja wykresów funkcji w szkolnym kursie matematyki

Głównym celem projektu jest rozwijanie umiejętności i zdolności uczniów w zakresie czytania i rysowania rysunków, w kształtowaniu racjonalnych metod samodzielnego działania.

Konieczność doskonalenia edukacji graficznej jako całości jest podyktowana nie tylko współczesnymi wymaganiami produkcyjnymi, ale także rolą grafiki w rozwoju myślenia technicznego i zdolności poznawczych uczniów. Zdolność człowieka do przetwarzania informacji graficznych jest jednym ze wskaźników jego rozwoju umysłowego. Dlatego szkolenie graficzne powinno stać się integralnym elementem ogólnego szkolenia edukacyjnego.

Wyniki

Tak więc opracowany projekt „Konstrukcja i transformacja grafów funkcyjnych”, poświęcony jednemu z centralnych pojęć matematyki - zależności funkcjonalnej, koncentruje się na usystematyzowaniu i poszerzeniu wiedzy uczniów. Badanie konkretnych metod przekształcania wykresów funkcji odbywa się w sposób analityczny i graficzny według ścisłych schematów metodologicznych. Zebrany materiał może być wykorzystany na zajęciach oraz do samokształcenia uczniów. Do prowadzenia zajęć można wykorzystać różnorodne formy i metody organizacji oraz szkolenia.